I had a chance, recently, to watch computer simulations and interact with a regional economic impact model called REMI. This is a multi-equation model of some vintage (dating back the 1980’s) that has continued to evolve. It’s probably currently the leader in the field and has seen recent application to assessing proposals for increasing the minimum wage – in California, Vermont, San Francisco – and to evaluating a carbon tax for the Citizen’s Climate Initiative (see the video presentation at the end of this post).
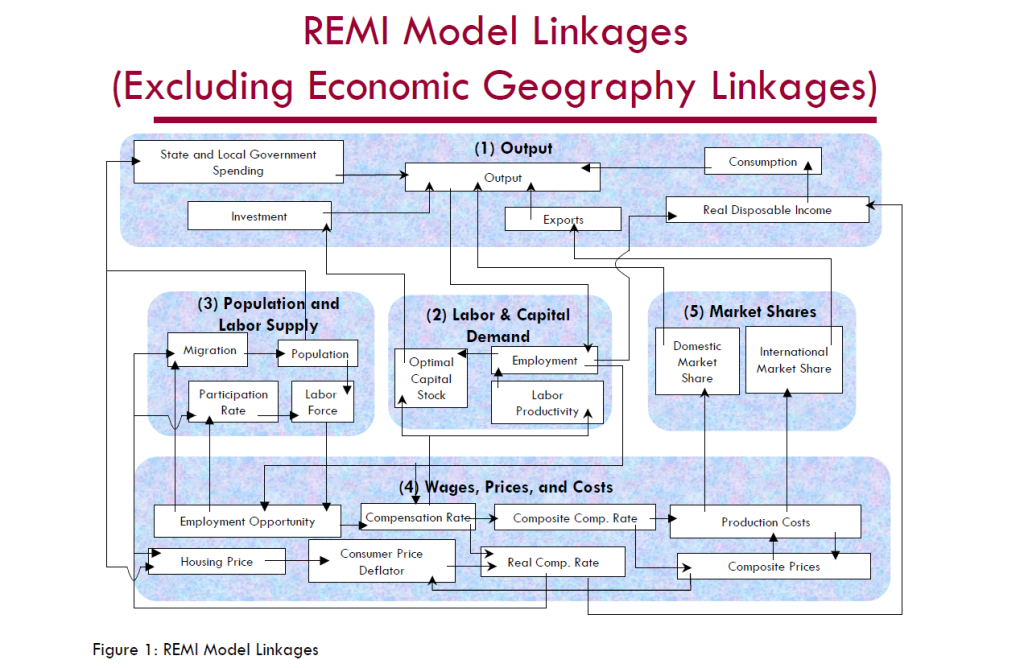
One way to interact with REMI is to click on blocks in a computer screen based on the following schematic
I watched Brian Lewandowski do this at Colorado University’s Leeds School of Business.
Brian set parameters for increases in labor productivity for professional services and changes in investment in primary and secondary educational by clicking on boxes or blocks. Brian, Richard Wobbekind (pictured below), and I discussed results, and how REMI is helpful in exploring “what-if’s” and might have applications to optimizing tax policies at the state level..
Wobbekind is himself a leader in preparing and presenting State-level forecasts for Colorado, and is active in the International Institute of Forecasters (IIF) which sponsors the International Journal of Forecasting and Foresight – as well as being an Associate Dean of CU’s Leeds School of Business.
Key Point About Multi-Equation, Multivariate Economic Models
From the standpoint of forecasting, the best way I can understand where REMI should be placed in the tool-kit is to remember the distinction between conditional and unconditional forecasts.
REMI model documentation indicates that,
The REMI model consists of thousands of simultaneous equations with a structure that is relatively straightforward. The exact number of equations used varies depending on the extent of industry, demographic, demand, and other detail in the specific model being used. The overall structure of the model can be summarized in five major blocks: (1) Output, (2) Labor and Capital Demand, (3) Population and Labor Supply, (4) Wages, Prices, and Costs, and (5) Market Shares
So you might have equations such as,
X1t = a0 + a1Z1t +..+ akZkt
X2t = b0 + b1Z1t +..+ brZrt
In order to predict unconditionally what (X1t,X2t) will be at some specific future time T*, it is necessary to correctly derive the parameters (a0,a1,..,ak,b0,b1,,…,br).
And it also is necessary, for an unconditional forecast, to predict the future values of all the exogenous variables on the right-hand side of the equation – that is all the Z variables that are not in fact X variables.
This usually means that unconditional forecasts from multivariate forecast models have wide and rapidly diverging confidence intervals.
Thus, if you try to forecast future employment in, say, California with such models, they may underperform simpler, single equation models – such as those based on exponential smoothing, for example.
This does not invalidate general systems models such as REMI.
Assuming the flows and linkages of sectors and blocks are realistic and correctly modeled, such models can help think through the consequences of policy decisions, new legislation, and infrastructure investments.
This is essentially to say that these models may present good conditional forecasts – basically “what-if’s” without being the best forecasting tool available.
Here is a video presentation based on the Citizen’s Climate Initiative application of REMI to assessing a carbon tax – an interesting proposal.