Here are some backtests of my new stock market forecasting procedures.
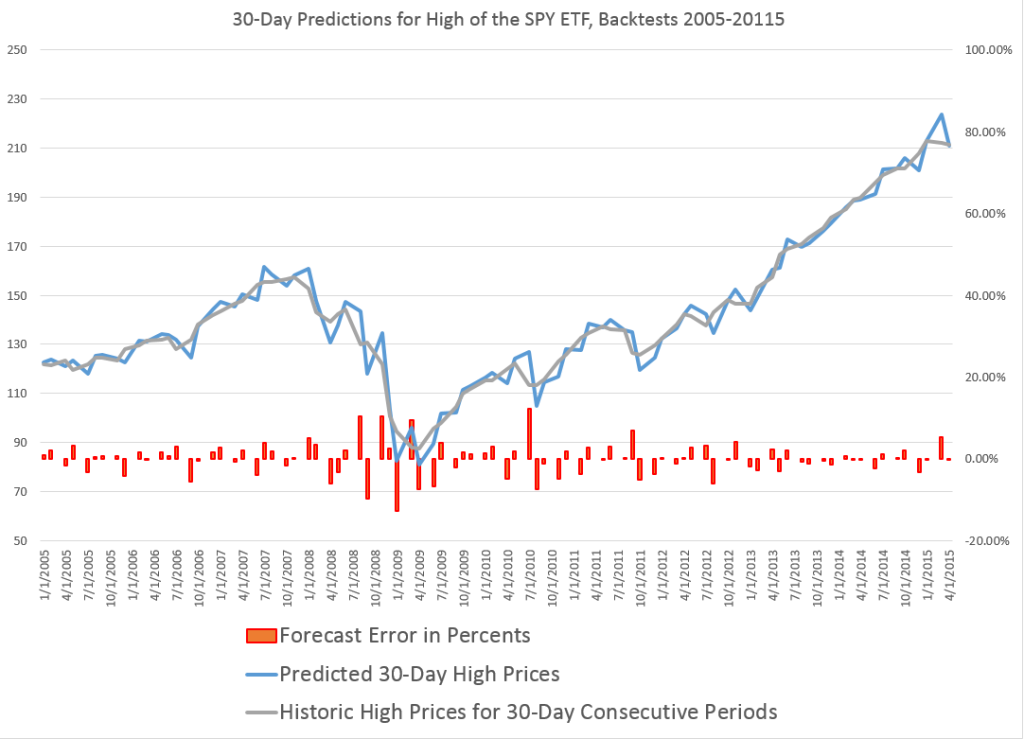
Here, for example, is a chart showing the performance of what I call the “proximity variable approach” in predicting the high price of the exchange traded fund SPY over 30 day forward periods (click to enlarge).
So let’s be clear what the chart shows.
The proximity variable approach- which so far I have been abbreviating as “PVar” – is able to identify the high prices reached by the SPY in the coming 30 trading days with forecast errors mostly under 5 percent. In fact, the MAPE for this approximately ten year period is 3 percent. The percent errors, of course, are charted in red with their metric on the axis to the right.
The blue line traces out the predictions, and the grey line shows the actual highs by 30 trading day period.
These results far surpass what can be produced by benchmark models, such as the workhorse No Change model, or autoregressive models.
Why not just do this month-by-month?
Well, months have varying numbers of trading days, and I have found I can boost accuracy by stabilizing the number of trading days considered in the algorithm.
Comments
Realize, of course, that a prediction of the high price that a stock or ETF will reach in a coming period does not tell you when the high will be reached – so it does not immediately translate to trading profits. The high in question could come with the opening price of the period, for example, leaving you out of the money, if you hear there is this big positive prediction of growth and then jump in the market.
However, I do think that market participants react to anticipated increases or decreases in the high or low of a security.
You might explain these results as follows. Traders react to fairly simple metrics predicting the high price which will be reached in the next period – and let this concept be extensible from a day to a month in this discussion. In so reacting, these traders tend to make such predictive models self-fulfilling.
Therefore, daily prices – the opening, the high, the low, and the closing prices – encode a lot more information about trader responses than is commonly given in the literature on stock market forecasting.
Of course, increasingly, scholars and experts are chipping away at the “efficient market hypothesis” and showing various ways in which stock market prices are predictable, or embody an element of predictability.
However, combing Google Scholar and other sources, it seems almost no one has taken the path to modeling stock market prices I am developing here. The focus in the literature is on closing prices and daily returns, for example, rather than high and low prices.
I can envision a whole research program organized around this proximity variable approach, and am drawn to taking this on, reporting various results on this blog.
If any readers would like to join with me in this endeavor, or if you know of resources which would be available to support such a project – feel free to contact me via the Comments and indicate, if you wish, whether you want your communication to be private.
1. We know that the high-low range is a volatility estimator
2. We know that volatility has time-series structure.
Is that what’s going on in your results?
Good question, and thanks for asking it.
You are right – the high/low range is a volatility estimator. Also, there is extensive econometric research on the time-series structure of volatility, for example the whole ARCH/GARCH family of methods.
But the proximity variable approach – which is what I am calling the methods used for these forecasts – is not closely related to these methods for modeling volatility.
So what I find is that the range – the difference between the high and the low in a period – is much more difficult to predict than, strangely, the midpoint of the range. I’m looking deeper into this apparent paradox, but it highlights the fact that these methods are not particularly good at forecasting the range, which is one metric for volatility.