Uncategorized

Outlook for 2021 – Early Perspective

Here is an update on the PowerPoint Deck from the St. Louis Federal Reserve databanks, focusing on the condition of the US economy.

CurrentSituationFeb2021 (1)Download

In general, things have recovered substantially from the rapid and deep dip in business activity in 2020, due to the lockdown and other aspects of the pandemic. Levels of production and consumption have not reached previous peaks in 2019 and 2020, however.

Optimism is in the air as the vaccines roll out. At the same time, there is talk many jobs have been lost for the longer term – especially in food, lodging and travel. Patterns of work may permanently change. More remote work lowering demand for offices. More retail moving online, impacting commercial real estate via the decline of shopping centers and retail outlets generally. Logistics and warehousing are growth areas of the economy.

Growing inequality is a troublesome feature. Many workers in food services, hotels, travel and retail have experienced joblessness, making paying the mortgage or even rent challenging. Food banks look to be doing a booming business. The closure of normal public school operation in many areas has impacted families depending, in some measure, on the school lunch programs.

On the other hand, the stock market sees new highs. Of course, only a small percentage of people own any significant number of stocks, so the efforts of the US Federal Reserve to bolster markets have very different impacts on groups of people in the US.

About 70 percent of US gross domestic product (GDP) is accounted for by consumer spending. It’s possible that the overhand from the pandemic could wing consumer spending later in 2021, if there is not substantial rebound in employment or significant government stimulus.

Uncategorized

Where We Are Fall 2020

The St. Louis Federal Reserve Bank supports an important data center called FRED.

The following slide deck is developed from macroeconomic and financial data updated through early July 2020. These 14 or so slides represent an important and historic resource. In almost every case, recent numbers are record-breaking – in the wrong way, unfortunately.

To summarize, more than 12 million jobs have been lost since the beginning of 2020, even with some rebound. Trillions of dollars of GDP have been foregone, and the Federal Budget Deficit has increased by several trillion dollars. The US Federal Reserve Bank has pumped in more than double the amount of liquidity in a few months, as it did in 2008-2009.

These slides set a Baseline. Where do we go from here?

CurrentSituationSept12020Download
Uncategorized

Predictions of High and Low Prices as Technical Indicators

Major retail stock trading platforms, like Charles Schwab or TDAmeritrade’s ThinkorSwim, provide convenient ways to throw up results of various technical stock price indicators to inform decisions about entering or exiting a trade. These technical indicators include, for example, the Relative Strength Index (RSI), fast and slow Stochastic Oscillators, various Moving Average Convergence Divergence (MACD) metrics, and On Board Volume (OBV). Investopedia provides good background on these.

So I want to initiate my sometime return to blogging by presenting research on a NEW TECHNICAL STOCK MARKET INDICATOR.

Here is a link to a presentation that highlights the Predicted Range as Technical Stock Indicator which can lead – with the SPDR S&P 500 exchange traded fund SPY – to results which beat Buy & Hold, even after capital gains are deducted on an annual basis from trading profits.

https://priceinfodynamics.com/wp-content/uploads/2020/06/Predictions-of-High-and-Low-Prices-as-Technical-Indicators.pdf

Contact me at [email protected] for more information about this new market indicator.

It basically just scratches the surface of what new insights to stock trading can be developed with suitably accurate predictions of high and low security prices over various periods.

forecasting research, Uncategorized

July 2020 – First New Post in While

Since my last post in 2017, I have hunkered down on a stock price forecasting idea and related trading system. With the help of several talented and dedicated persons over these years, we basically “got it.” What we created can be looked at as a “new paradigm” in stock trading – nothing less than that.

While I intend to evangelize this in coming posts, let’s first recognize startling developments since 2017 – with respect to the global economy, business forecasting and forecasting behavior more generally (e.g. predicting spread of COVID-19).

Google Analytics pinged me recently to note that tens of thousands visited this site in 2019 – even though posts stopped in 2017.

So here are some impressions.

First, the numbers for unemployment and impact of GDP from March 2020 on look like they are “off the charts.” Nothing has happened quite like the lockdown in the US, China, Korea, Japan, and many European countries.

As a secondary consequence, growth in liabilities of the Federal Reserve bank and the US deficit also are “off the charts.” Hockey stick movements up.

Meanwhile, the US stock market, probably because of massive injections of “liquidity” by the US Federal Reserve, has, as of this writing, nearly recovered peak levels seen before the February 2020 correction.

“Dr. Doom” – Professor Nouriel Roubini of New York University is back at it – predicting a decade of depression 2021 and later.

In short, this is a situation where there is a growing demand for some type of forward guidance, some predictions of what is going to happen.

My time resources for providing a public perspective on this are limited – but I think it does make sense to keep this blog moving forward.

Keep checking, and eventually, we will set up means to get notifications.

Stay safe and stay well.

forecasting trade balances, global supply chains, structure of international trade

What Mr. Trump May Be Thinking About US Trade

1 Comment

It’s often said a few pictures are worth thousands of words. But pictures can be a little misleading, when everything is globally interconnected.

First, look at the standard view of the ever-widening US trade deficit and negative US balance of payments. Then, focusing on Mexico – a Trump whipping boy – let’s pry open the box and look inside to see what is traded back and forth. What the numbers suggest is that the greatest part of the US trade deficit is involved with “trade by related parties”, i.e. multinational companies importing parts and other goods to the US, sometimes for assembly here and export. Many of these are US companies who have used international operations to cut production costs, but then gain access to US customers on favorable terms through their time-honored sales channels.

The Standard Picture

Just looking at the standard US trade statistics, the story is grim. Imports to the US have persistently exceeded US exports since the 1980’s, with the negative balance soaring just before the Great Recession of 2008-2009 to around $200 billion.

Four countries, China, Germany, Mexico, and Japan are the largest contributors to the US trade deficit, as the following chart shows.

Sharp erosion in the US balance of international payments accompanies these import and export curves.

But What Does Mexico Import Into the US?

This is where we have to adopt a new way of looking at these facts.

So, in recent years, US Trade authorities have begun to maintain a new kind of statistical data, relating to trade by related parties, a.k.a. trade between parts of the same (multinational) company.

Mexico, in fact, has a large portion of this trade by related parties, as the following Table indicates.

Readers may also want to consult J.W. Mason’s The Slack Wire What Exactly Does Mexico Export to the US? 

Now there are all sorts of measurement issues involved in measuring trade by related parties, and, of course, the import prices for within-company trade can be somewhat suspect.

But, its interesting some years ago, the Middle Class Political Economist calculated that –

Thus, things are more complicated than suggested by trade in wine from Portugal and textiles from Old Blighty.

In fact, a scholar at Harvard has one of the most compelling pictures highlighting the global supply chain.

Thus, the 787 Development Team encompasses 50 suppliers located in 9 countries (Australia, France, Germany, Italy, Japan, Korea, Sweden, the United Kingdom and the United States). 70 percent of the 787s parts are produced abroad.

 From Pol Antras’ CREI Lectures in Macroeconomics Contracts and the Global Organization of Production, June 2012

So, this is the sort of complexity which enfuriates the “stranded white working class,” left behind when the factories move abroad, but the company marketing organization builds new offices in the nearby metropole.

From which I also deduce that the conflict between Mr. Trump, Mr. Bannon, and powerful interests on the other side is likely to be a serious battle. This is not a win-win, as global trade always was presented (even though it has “distributional impacts”). Border taxes will intervene in these global commodity chains which have been constructed to further the pursuit of profits by multinationals. So border taxes will in fact also have distributional consequences, but these impacts will extend to company profits and involve reorganization of production.

I mean this is like going to be a pitched battle.

gasoline price forecasts, impacts of offshoring, macroeconomic forecasting

What Up? The Trump Years – I

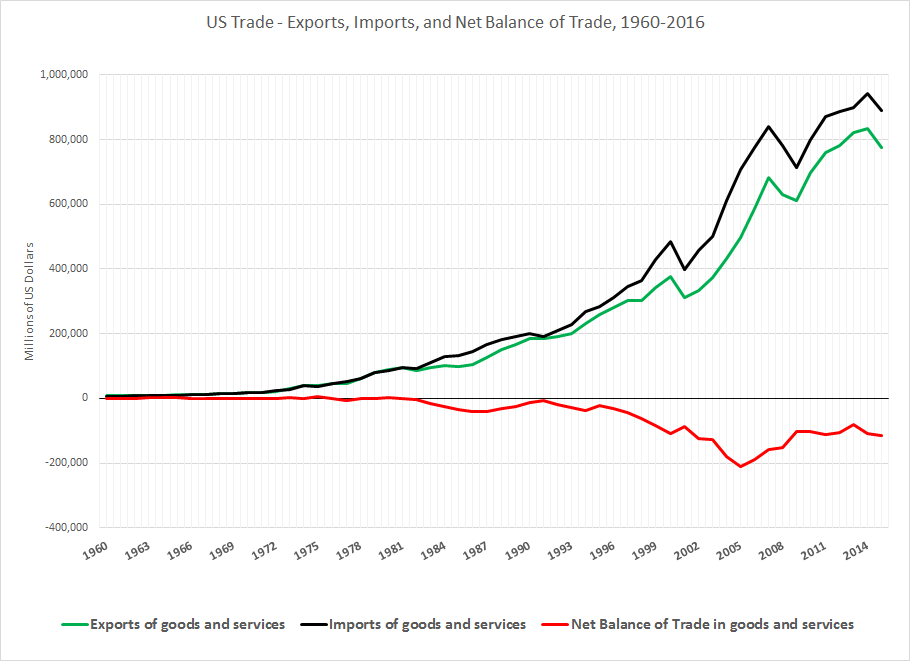
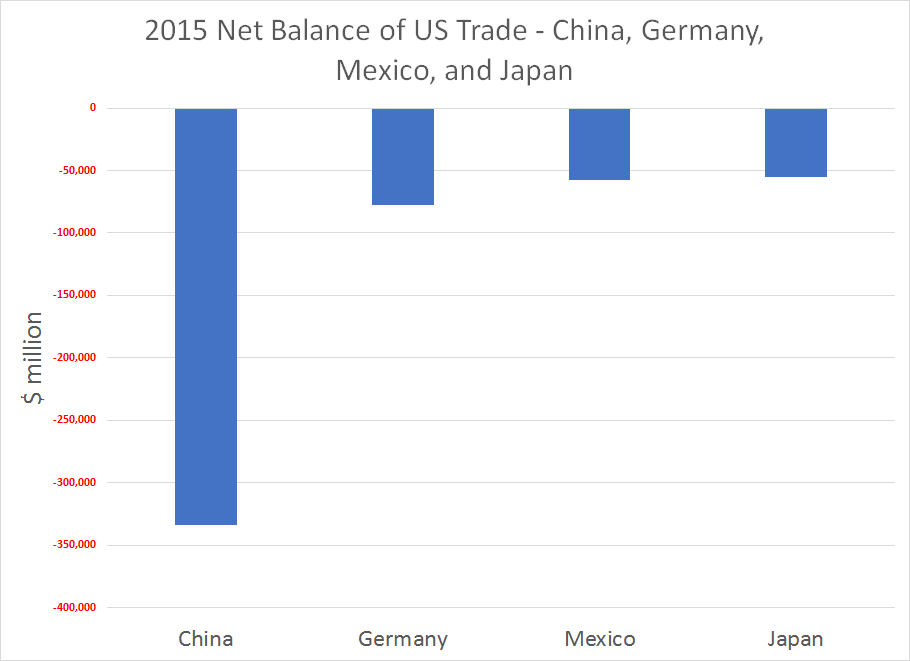
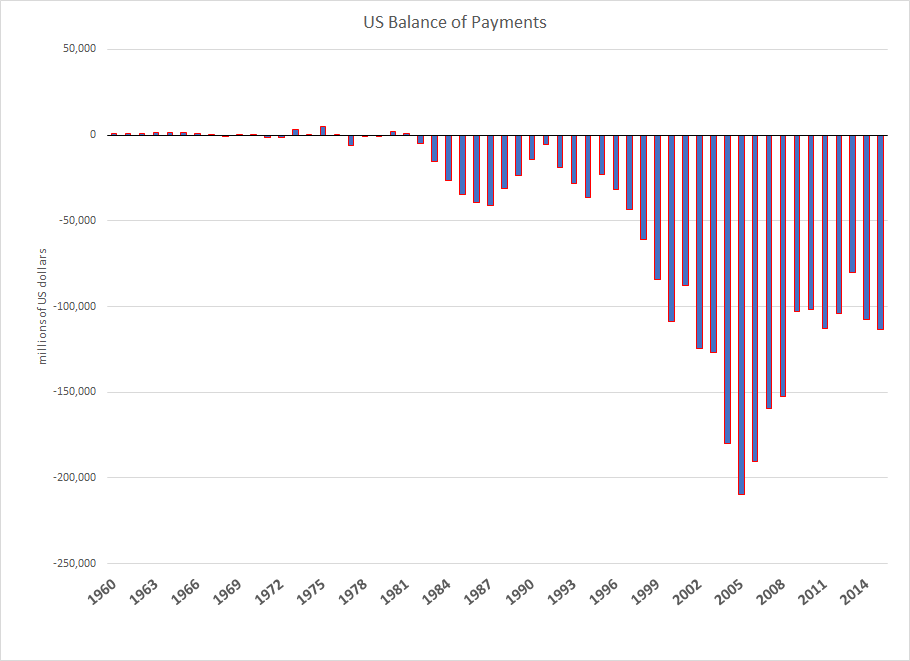
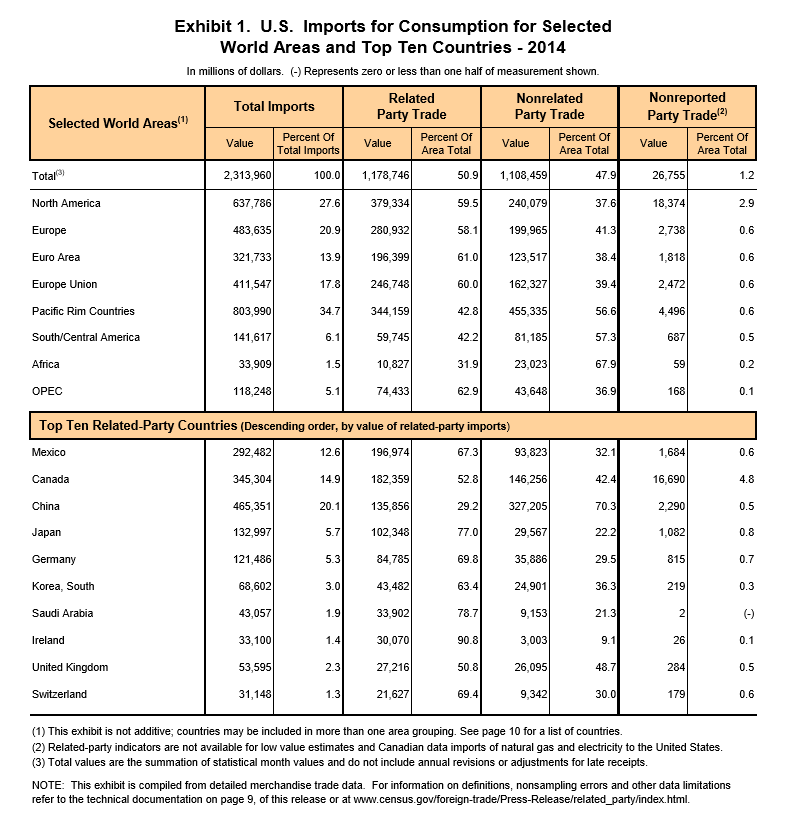
From the standpoint of business forecasting, Donald Trump is important. His challenge to various conventional wisdoms and apparently settled matters raises questions about where things will go in 2017 and beyond. Furthermore, his style of governance is unknown, since as a businessman and minor celebrity, Trump has literally no government experience. He is an Outsider to the political scene, arriving with a portfolio of ideas like mass deportations of illegal immigrants, a massive wall between the United States and its southern neighbor, Mexico, bringing manufacturing jobs back, no further gun controls, and more rigorous screening of immigrants from the Middle East and Muslim countries.

So, with Donald Trump’s Inauguration January 20, a lot seems up in the air. But behind the hoopla, fundamental economic processes and trends are underway. What types of forecasts, therefore, seem reasonable, defensible?

Some Thoughts on Economics

Let’s start with economics.

Donald Trump could be the President who returns inflation and higher interest rates to the equation.

Offshoring and outsourcing have been factors in creating industrial wastelands and hollowed out production in the US – areas where you can drive for miles through abandoned buildings and decaying business centers. At the same time, offshoring and outsourcing bring low-cost electronics and other products to US consumers.

It is a Faustian bargain. If you were a wage-earner with a high school education (or less), supporting a family working in the “fast food sector” or convenience store, maybe holding two jobs to patch together enough income for bills – what you got was a $500 big screen TV and all sorts of gadgets for your kids. You could buy a cheap computer, and cheap clothing, too. Credit cards are available, although less so after 2008.

Oh yeah, another place you could work is in a Big Box store, whose long aisles and vanishing sakes clerks serve as the terminus of global supply chains coursing through ports on the West and East coasts. These are the ports where box-car size containers from China and elsewhere are unloaded, and put on rail cars or moved by truck to stores where consumers can purchase the goods packed in these containers largely on credit.

Is it even possible to slow, stop, or reverse this dynamic?

Let’s see, the plan for bringing manufacturing back to the United States involves deregulation of business, making doing business in the US more profitable. One idea that has been floated is that deregulation would provide incentives for US business to repatriate all that money they are holding overseas back to the US, where it could be invested in America.

Before taking office, President-elect Trump earned points with his supporters by “jawboning” US and foreign companies to keep jobs here, threatening taxes or fees for re-importing stuff to the US from newly relocated operations.

But most of the returning manufacturing would be highly capital intensive (think”robots”) so that only a few more jobs could be garnered from this re-investment in America, right?

Well, before dismissing the idea, note that some of these new jobs would be good-paying, probably requiring higher skills to run more automated production processes.

But this is a different game – producing in the United States, discouraging companies to move operations abroad to lower cost environments, placing taxes, fees, or tariffs on goods manufactured abroad coming into the US. This also involves higher prices.

There is another thread, though, to do with the impact of “deregulation” on the US oil and gas industry, aka “fracking.”

When American ingenuity developed hydraulic fracturing technology (“fracking”) to tap lower yield oil and gas reserves in areas of Texas, South Dakota, and elsewhere, US oil and gas production surged almost to the point of self-sufficiency. But then the Saudi’s lowered the boom, and oil prices dropped, making the higher cost US wells unprofitable, and slowing their expansion.

Before that happened, however, it was apparent fracking in the West and the older oil fields of the Eastern US energized activity up the supply chain, drawing forth significant manufacturing of pipes and equipment. The proverbial boom towns cropped up in the Dakotas and Texas, where hours of work could be long, and pay was good.

Clearly, as oil prices rise again with various global geopolitical instabilities, the US oil and gas industry can rise again, create large numbers of jobs and, also, significant environmental degradation – unless done with high standards for controlling wastes and methane emissions.

But Mr. Trump nominated the former Oklahoma Attorney General to head the US Environmental Protection Agency (EPA) – an agency which Mr. Trump vowed at one point in the campaign to eliminate and which his nominee Scott Pruitt fought tooth and nail in the courts.

So, concern with the environment to the winds, there is a case for a Trump “boom” in 2017 and 2018 – if global oil prices can stay above the breakeven point for US oil and gas production.

Another thread or storyline ties in here  – deportations and stronger controls over illegal immigration.

Again, we have to consider how things are actually made, and we see that, as Anthony Bourdain has noted, many of the restaurant jobs in New York City and other big cities  – in the kitchen especially – are filled by new migrants, many not here legally.

Also, scores of construction jobs in the Rocky Mountain West are filled by Hispanic workers.

Pressure on these working populations to produce their papers can only lead to higher wages and costs, which will be passed along to consumers.

And don’t forget President Trump’s promise to restore US military preparedness. As “cost-plus” contracts, US defense production acts as a conduit for price increases, and may be overpriced (the alternative being to let potential enemies manufacture US weapons).

So what this thought experiment suggests is that, initially, jobs in the Trump era may be boosted by captive or returning manufacturing operations and resumption of the US oil and gas boom – but be accompanied by higher prices. Higher prices also are thematic to limiting the labor pool in US industries, and the cost-overruns are endemic to US defense production.

This is not the end of the economics story, obviously.

The next thing to consider is the US Federal Reserve Bank, which, under Chairman Yellen and other members of the Board of Governors is itching to increase interest rates, as the US economy recovers.

Witnessing a surge of employment from fracking jobs plus a smatter of repatriation of US manufacturing, and the associated higher prices involved with all of this, the Fed should have plenty of excuse to bring interest rates back to historic levels.

Will this truncate the Trump boom?

And what about international response to these developments in the United States?

financial forecasting, stock market forecasts

Daily High and Low Stock Prices – Falling Knives

The mathematics of random walks form the logical underpinning for the dynamics of prices in stock, currency, futures, and commodity markets.

Once you accept this, what is really interesting is to consider departures from random walk movements of prices. Such distortions can signal underlying biases brought to the table by investors and others with influence in these markets.

“Falling knives” may be an example.

A good discussion is presented in Falling Knives: Do Stocks Really Drop 3 Times Faster Than They Rise?

This article in Seeking Alpha is more or less organized around the following chart.

FallingKnives

The authors argue this classic chart is really the result of a “Black Swan” event – namely the Great Recession of 2008-2009. Outside of unusual deviations, however, they try to show that “the rate of rallies and pullbacks are approximately equal.”

I’ve been exploring related issues and presently am confident that there are systematic differences in the volatility of high and low prices over a range of time periods.

This seems odd to say, since high and low prices exist within the continuum of prices, their only distinguishing feature being that they are extreme values over the relevant interval – a trading day or collection of trading days.

However, the variance or standard deviation of daily percent changes or rates of change of high and low prices are systematically different for high and low prices in many examples I have seen.

Consider, for example, rates of change of daily high and low prices for the SPY exchange traded fund (ETF) – the security charted in the preceding graph.

RollingSTDEV

This chart shows the standard deviation of daily rates of change of high and low prices for the SPY over rolling annual time windows.

This evidence suggests higher volatility for daily growth or rates of change of low prices is more than something linked just with “Black Swan events.”

Thus, while the largest differences between standard deviations occur in late 2008 through 2009 – precisely the period of the financial crisis – in 2011 and 2012, as well as recently, we see the variance of daily rates of change of low prices significantly higher than those for high prices.

The following chart shows the distribution of these standard deviations of rates of change of daily high and low prices.

STDEVDist

You can see the distribution of the daily growth rates for low prices – the blue line – is fatter in a certain sense, with more instances of somewhat greater standard deviations than the daily growth rates for high prices. As a consequence, too, the distribution of the daily growth rates of low prices shows less concentration near the modal value, which is sharply peaked for both curves.

These are not Gaussian or normal distributions, of course. And I find it interesting that the finance literature, despite decades of recognition of these shapes, does not appear to have a consensus on exactly what types of distributions these are. So I am not going to jump in with my two bits worth, although I’ve long thought that these resemble Laplace Distributions.

In any case, what we have here is quite peculiar, and can be replicated for most of the top 100 ETF’s by market capitalization. The standard deviation of rates of change of current low price to previous low prices generally exceeds the standard deviation of rates of change of high prices, similarly computed.

Some of this might be arithmetic, since by definition high prices are greater numerically than low prices, and we are computing rates of change.

However, it’s easy to dispel the idea that this could account for the types of effects seen with SPY and other securities. You can simulate a random walk, for example, and in thousands of replications with positive prices essentially lose any arithmetic effect of this type in noise.

I believe there is more to this, also.

For example, I find evidence that movements of low prices lead movements of high prices over some time frames.

Investor psychology is probably the most likely explanation, although today we have to take into account the “psychology” of robot trading algorithms. Presumeably, these reflect, in some measure, the predispositions of their human creators.

It’s kind of a puzzle.

Top image from SGS Swinger BlogSpot

Deep Questions, financial forecasting, Janet Yellen outlook

The Apostle of Negative Interest Rates

Miles Kimball is a Professor at the University of Michigan, and a vocal and prolific proponent of negative interest rates. His Confessions of a Supply-Side Liberal is peppered with posts on the benefits of negative interest rates.

March 2 Even Central Bankers Need Lessons on the Transmission Mechanism for Negative Interest Rates, after words of adoration, takes the Governor of the Bank of England (Mark Carney) to task. Carney’s problem? Carney wrote recently that unless regular households face negative interest rates in their deposit accounts.. negative interest rates only work through the exchange rate channel, which is zero-sum from a global point of view.

Kimball’s argument is a little esoteric, but promotes three ideas.

First, negative interest rates central bank charge member banks on reserves should be passed onto commercial and consumer customers with larger accounts – perhaps with an exemption for smaller checking and savings accounts with, say, less than $1000.

Second, moving toward electronic money in all transactions makes administration of negative interest rates easier and more effective. In that regard, it may be necessary to tax transactions conducted in paper money, if a negative interest rate regime is in force.

Third, impacts on bank profits can be mitigated by providing subsidies to banks in the event the central bank moved into negative interest rate territory.

Fundamentally, Kimball’s view is that.. monetary policy–and full-scale negative interest rate policy in particular–is the primary answer to the problem of insufficient aggregate demand. No need to set inflation targets above zero in order to get the economy moving. Just implement sufficiently negative interest rates and things will rebound quickly.

Kimball’s vulnerability is high mathematical excellence coupled with a casual attitude toward details of actual economic institutions and arrangements.

For example, in his Carney post,  Kimball offers this rather tortured prose under the heading -“Why Wealth Effects Would Be Zero With a Representative Household” –

It is worth clarifying why the wealth effects from interest rate changes would have to be zero if everyone were identical [sic, emphasis mine]. In aggregate, the material balance condition ensures that flow of payments from human and physical capital have not only the same present value but the same time path and stochastic pattern as consumption. Thus–apart from any expansion of the production of the economy as a whole as a result of the change in monetary policy–any effect of interest rate changes on the present value of society’s assets overall is cancelled out by the effect of interest rate changes on the present value of the planned path and pattern of consumption. Of course, what is actually done will be affected by the change in interest rates, but the envelope theorem says that the wealth effects can be calculated based on flow of payments and consumption flows that were planned initially.

That’s in case you worried a regime of -2 percent negative interest rates – which Kimball endorses to bring a speedy end to economic stagnation – could collapse the life insurance industry or wipe out pension funds.

And this paragraph is troubling from another standpoint, since Kimball believes negative interest rates or “monetary policy” can trigger “expansion of the production of the economy as a whole.” So what about those wealth effects?

Indeed, later in the Carney post he writes,

..for any central bank willing to go off the paper standard, there is no limit to how low interest rates can go other than the danger of overheating the economy with too strong an economic recovery. If starting from current conditions, any country can maintain interest rates at -7% or lower for two years without overheating its economy, then I am wrong about the power of negative interest rates. But in fact, I think it will not take that much. -2% would do a great deal of good for the eurozone or Japan, and -4% for a year and a half would probably be enough to do the trick of providing more than enough aggregate demand.

At the end of the Carney post, Kimball links to a list of his and other writings on negative interest rates called How and Why to Eliminate the Zero Lower Bound: A Reader’s Guide. Worth bookmarking.

Here’s a YouTube video.

Although not completely fair, I have to say all this reminds me of a widely-quoted passage from Keynes’ General Theory –

“Practical men who believe themselves to be quite exempt from any intellectual influence, are usually the slaves of some defunct economist. Madmen in authority, who hear voices in the air, are distilling their frenzy from some academic scribbler of a few years back”

Of course, the policy issue behind the spreading adoption of negative interest rates is that the central banks of the world are, in many countries, at the zero bound already. Thus, unless central banks can move into negative interest rate territory, governments are more or less “out of ammunition” when it comes to combatting the next recession – assuming, of course, that political alignments currently favoring austerity over infrastructure investment and so forth, are still in control.

The problem I have might be posed as one of “complexity theory.”

I myself have spent hours pouring over optimal control models of consumption  and dynamic general equilibrium. This stuff is so rarified and intellectually challenging, really, that it produces a mindset that suggests mastery of Portryagin’s maximum principle in a multi-equation setup means you have something relevant to say about real economic affairs. In fact, this may be doubtful, especially when the linkages between organizations are so complex, especially dynamically.

The problem, indeed, may be institutional but from a different angle. Economics departments in universities have, as their main consumer, business school students. So economists have to offer something different.

One would hope machine learning, Big Data, and the new predictive analytics, framed along the lines outlined by Hal Varian and others, could provide an alternative paradigm for economists – possibly rescuing them from reliance on adjusting one number in equations that are stripped of the real, concrete details of economic linkages.

financial forecasts

Negative Interest Rates

What are we to make of negative interest rates?

Burton Malkiel (Princeton) writes in the Library of Economics and Liberty that – The rate of interest measures the percentage reward a lender receives for deferring the consumption of resources until a future date. Correspondingly, it measures the price a borrower pays to have resources now.

So, in a topsy-turvy world, negative interest rates might measure the penalty a lender receives for delaying consumption of resources to some future date from a more near-term date, or from now.

This is more or less the idea of this unconventional monetary policy, now taking hold in the environs of the European and Japanese Central Banks, and possibly spreading sometime soon to your local financial institution. Thus, one of the strange features of business behavior since the Great Recession of 2008-2009 has been the hoarding of cash either in the form of retained corporate earnings or excess bank reserves.

So, in practical terms, a negative interest rate flips the relation between depositors and banks.

With negative interest rates, instead of receiving money on deposits, depositors must pay regular sums, based on the size of their deposits, to keep their money with the bank.

“If rates go negative, consumer deposit rates go to zero and PNC would charge fees on accounts.”

The Bank of Japan, the European Central Bank and several smaller European authorities have ventured into this once-uncharted territory recently.

Bloomberg QuickTake on negative interest rates

The Bank of Japan surprised markets Jan. 29 by adopting a negative interest-rate strategy. The move came 1 1/2 years after the European Central Bank became the first major central bank to venture below zero. With the fallout limited so far, policy makers are more willing to accept sub-zero rates. The ECB cut a key rate further into negative territory Dec. 3, even though President Mario Draghi earlier said it had hit the “lower bound.” It now charges banks 0.3 percent to hold their cash overnight. Sweden also has negative rates, Denmark used them to protect its currency’s peg to the euro and Switzerland moved its deposit rate below zero for the first time since the 1970s. Since central banks provide a benchmark for all borrowing costs, negative rates spread to a range of fixed-income securities. By the end of 2015, about a third of the debt issued by euro zone governments had negative yields. That means investors holding to maturity won’t get all their money back. Banks have been reluctant to pass on negative rates for fear of losing customers, though Julius Baer began to charge large depositors.

These developments have triggered significant criticism and concern in the financial community.

Japan’s Negative Interest Rates Are Even Crazier Than They Sound

The Japanese government got paid to borrow money for a decade for the first time, selling 2.2 trillion yen ($19.5 billion) of the debt at an average yield of minus 0.024 percent on Tuesday…

The central bank buys as much as 12 trillion yen of the nation’s government debt a month…

Life insurance companies, for instance, take in premiums today and invest them to be able to cover their obligations when policyholders eventually die. They price their policies on the assumption of a mid-single-digit positive return on their bond portfolios. Turn that return negative and all of a sudden the world’s life insurers are either unprofitable or insolvent. And that’s a big industry.

Pension funds, meanwhile, operate the same way, taking in and investing contributions against future obligations. Many US pension plans are already borderline broke, and in a NIRP environment they’ll suffer a mass extinction. Again, big industry, many employees, huge potential impact on both Wall Street and Main Street.

It has to be noted, however, that real (or inflation-adjusted) interest rates have gone below zero already for certain asset classes. Thus, a highlight of the Bank of England Study on negative interest rates circa 2013 is this chart, showing the emergence of negative real interest rates.

NegRealIR

Are these developments the canary in the mine?

We really need some theoretical analysis from the economics community – perspectives that encompass developments like the advent of China as a major player in world markets and patterns of debt expansion and servicing in the older industrial nations.

Sales and new product forecasting in data-limited (real world) contexts