Category Archives: financial risk management

financial risk management, stock trading algorithms, Uncategorized

Portfolio Analysis

Greetings again. Took a deep dive into portfolio analysis for a colleague.

Portfolio analysis, of course, has been deeply influenced by Modern Portfolio Theory (MPT) and the work of Harry Markowitz and Robert Merton, to name a couple of the giants in this field.

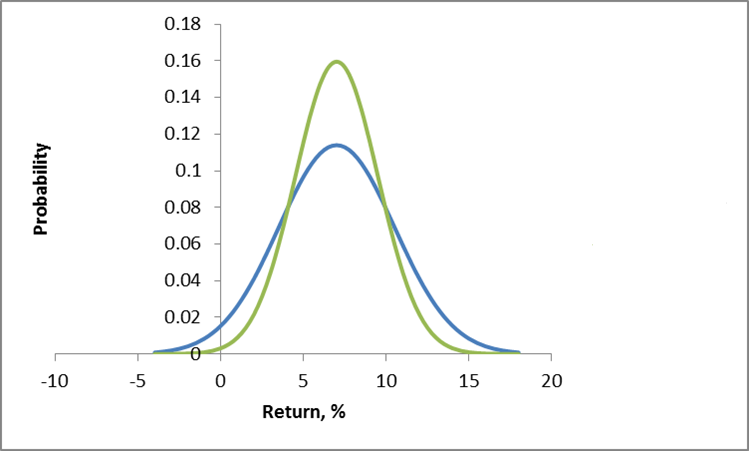
Conventionally, investment risk is associated with the standard deviation of returns. So one might visualize the dispersion of actual returns for investments around expected returns, as in the following chart.

investmentrisk

Here, two investments have the same expected rate of return, but different standard deviations. Viewed in isolation, the green curve indicates the safer investment.

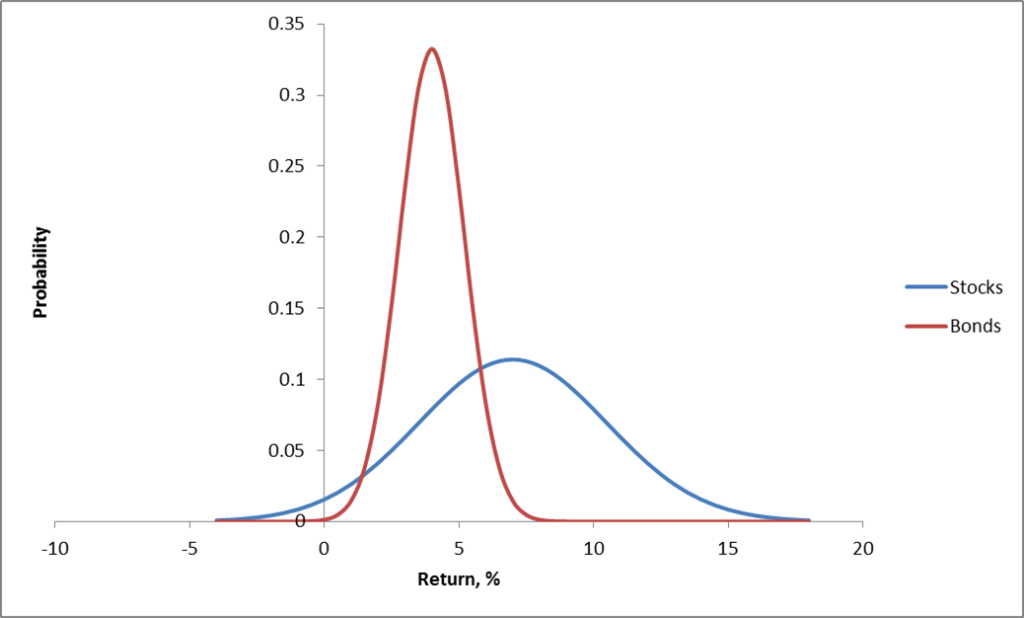
More directly relevant for portfolios are curves depicting the distribution of typical returns for stocks and bonds, which can be portrayed as follows.

stocksbonds

Now the classic portfolio is comprised of 60 percent stocks and 40 percent bonds.

Where would its expected return be? Well, the expected value of a sum of random variables is the sum of their expected values. There is an algebra of expectations to express this around the operator E(.). So we have E(.6S+.4B)=.6E(S)+.4E(B), since a constant multiplied into a random variable just shifts the expectation by that factor. Here, of course, S stands for “stocks” and B “bonds.”

Thus, the expected return for the classic 60/40 portfolio is less than the returns that could be expected from stocks alone.

But the benefit here is that the risks have been reduced, too.

Thus, the variance of the 60/40 portfolio usually is less than the variance of a portfolio composed strictly of stocks.

One of the ways this is true is when the correlation or covariation of stocks and bonds is negative, as it has been in many periods over the last century. Thus, high interest rates mean slow to negative economic growth, but can be associated with high returns on bonds.

Analytically, this is because the variance of the sum of two random variables is the sum of their variances, plus their covariance multiplied by a factor of 2.

Thus, algebra and probability facts underpin arguments for investment diversification. Pick investments which are not perfectly correlated in their reaction to events, and your chances of avoiding poor returns and disastrous losses can be improved.

Implementing MPF

When there are more than two assets, you need computational help to implement MPT portfolio allocations.

For a general discussion of developing optimal portfolios and the efficient frontier see http://faculty.washington.edu/ezivot/econ424/portfoliotheorymatrixslides.pdf

There are associated R programs and a guide to using Excel’s Solver with this University of Washington course.

Also see Package ‘Portfolio’.

These programs help you identify the minimum variance portfolio, based on a group of assets and histories of their returns. Also, it is possible to find the minimum variance combination from a designated group of assets which meet a target rate of return, if, in fact, that is feasible with the assets in question. You also can trace out the efficient frontier – combinations of assets mapped in a space of returns and variances. These assets in each case have expected returns on the curve and are minimum variance compared with all other combinations that generate that rate of return (from your designated group of assets).

One of the governing ideas is that this efficient frontier is something an individual investor might travel along as they age – going from higher risk portfolios when they are younger, to more secure, lower risk portfolios, as they age.

Issues

As someone who believes you don’t really know something until you can compute it, it interests me that there are computational issues with implementing MPT.

I find, for example, that the allocations are quite sensitive to small changes in expected returns, variances, and the underlying covariances.

One of the more intelligent, recent discussions with suggested “fixes” can be found in An Improved Estimation to Make Markowitz’s Portfolio Optimization Theory Users Friendly and Estimation Accurate with Application on the US Stock Market Investment.

The more fundamental issue, however, is that MPT appears to assume that stock returns are normally distributed, when everyone after Mandelbrot should know this is hardly the case.

Again, there is a vast literature, but a useful approach seems to be outlined in Modelling in the spirit of Markowitz portfolio theory in a non-Gaussian world. These authors use MPT algorithms as the start of a search for portfolios which minimize value-at-risk, instead of variances.

Finally, if you want to cool off and still stay on point, check out the 2014 Annual Report of Berkshire Hathaway, and, especially, the Chairman’s Letter. That’s Warren Buffett who has truly mastered an old American form which I believe used to be called “cracker barrel philosophy.” Good stuff.

accuracy of forecasts, derivatives markets, financial forecasting, financial risk management

Interest Rates – Forecasting and Hedging

A lot relating to forecasting interest rates is encoded in the original graph I put up, several posts ago, of two major interest rate series – the federal funds and the prime rates.

IratesFRED1

This chart illustrates key features of interest rate series and signals several important questions. Thus, there is relationship between a very short term rate and a longer term interest rates – a sort of two point yield curve. Almost always, the federal funds rate is below the prime rate. If for short periods this is not the case, it indicates a radical reversion of the typical slope of the yield curve.

Credit spreads are not illustrated in this figure, but have been shown to be significant in forecasting key macroeconomic variables.

The shape of the yield curve itself can be brought into play in forecasting future rates, as can typical spreads between interest rates.

But the bottom line is that interest rates cannot be forecast with much accuracy beyond about a two quarter forecast horizon.

There is quite a bit of research showing this to be true, including –

Professional Forecasts of Interest Rates and Exchange Rates: Evidence from the Wall Street Journal’s Panel of Economists

We use individual economists’ 6-month-ahead forecasts of interest rates and exchange rates from the Wall Street Journal’s survey to test for forecast unbiasedness, accuracy, and heterogeneity. We find that a majority of economists produced unbiased forecasts but that none predicted directions of changes more accurately than chance. We find that the forecast accuracy of most of the economists is statistically indistinguishable from that of the random walk model when forecasting the Treasury bill rate but that the forecast accuracy is significantly worse for many of the forecasters for predictions of the Treasury bond rate and the exchange rate. Regressions involving deviations in economists’ forecasts from forecast averages produced evidence of systematic heterogeneity across economists, including evidence that independent economists make more radical forecasts

Then, there is research from the London School of Economics Interest Rate Forecasts: A Pathology

In this paper we have demonstrated that, in the two countries and short data periods studied, the forecasts of interest rates had little or no informational value when the horizon exceeded two quarters (six months), though they were good in the next quarter and reasonable in the second quarter out. Moreover, all the forecasts were ex post and, systematically, inefficient, underestimating (overestimating) future outturns during up (down) cycle phases. The main reason for this is that forecasters cannot predict the timing of cyclical turning points, and hence predict future developments as a convex combination of autoregressive momentum and a reversion to equilibrium

Also, the Chapter in the Handbook of Forecasting Forecasting interest rates is relevant, although highly theoretical.

Hedging Interest Rate Risk

As if in validation of this basic finding – beyond about two quarters, interest rate forecasts generally do not beat a random walk forecast – interest rate swaps, are the largest category of interest rate contracts of derivatives, according to the Bank of International Settlements (BIS).

BIStable

Not only that, but interest rate contracts generally are, by an order of magnitude, the largest category of OTC derivatives – totaling more than a half a quadrillion dollars as of the BIS survey in July 2013.

The gross value of these contracts was only somewhat less than the Gross Domestic Product (GDP) of the US.

A Bank of International Settlements background document defines “gross market values” as follows;

Gross positive and negative market values: Gross market values are defined as the sums of the absolute values of all open contracts with either positive or negative replacement values evaluated at market prices prevailing on the reporting date. Thus, the gross positive market value of a dealer’s outstanding contracts is the sum of the replacement values of all contracts that are in a current gain position to the reporter at current market prices (and therefore, if they were settled immediately, would represent claims on counterparties). The gross negative market value is the sum of the values of all contracts that have a negative value on the reporting date (ie those that are in a current loss position and therefore, if they were settled immediately, would represent liabilities of the dealer to its counterparties).  The term “gross” indicates that contracts with positive and negative replacement values with the same counterparty are not netted. Nor are the sums of positive and negative contract values within a market risk category such as foreign exchange contracts, interest rate contracts, equities and commodities set off against one another. As stated above, gross market values supply information about the potential scale of market risk in derivatives transactions. Furthermore, gross market value at current market prices provides a measure of economic significance that is readily comparable across markets and products.

Clearly, by any account, large sums of money and considerable exposure are tied up in interest rate contracts in the over the counter (OTC) market.

A Final Thought

This link between forecastability and financial derivatives is interesting. There is no question but that, in practical terms, business is putting eggs in the basket of managing interest rate risk, as opposed to refining forecasts – which may not be possible beyond a certain point, in any case.

What is going to happen when the quantitative easing maneuvers of central banks around the world cease, as they must, and long term interest rates rise in a consistent fashion? That’s probably where to put the forecasting money.

anatomy of an asset bubble, asset bubbles, celebrity forecasters, financial forecasts, financial risk management, forecasting asset bubbles, forecasting research, forecasting turning points, stock market forecasts

Didier Sornette – Celebrity Bubble Forecaster

Professor Didier Sornette, who holds the Chair in Entreprenuerial Risks at ETH Zurich, is an important thinker, and it is heartening to learn the American Association for the Advancement of Science (AAAS) is electing Professor Sornette a Fellow.

It is impossible to look at, say, the historical performance of the S&P 500 over the past several decades, without concluding that, at some point, the current surge in the market will collapse, as it has done previously when valuations ramped up so rapidly and so far.

S&P500recent

Sornette focuses on asset bubbles and has since 1998, even authoring a book in 2004 on the stock market.

At the same time, I think it is fair to say that he has been largely ignored by mainstream economics (although not finance), perhaps because his training is in physical science. Indeed, many of his publications are in physics journals – which is interesting, but justified because complex systems dynamics cross the boundaries of many subject areas and sciences.

Over the past year or so, I have perused dozens of Sornette papers, many from the extensive list at http://www.er.ethz.ch/publications/finance/bubbles_empirical.

This list is so long and, at times, technical, that videos are welcome.

Along these lines there is Sornette’s Ted talk (see below), and an MP4 file which offers an excellent, high level summary of years of research and findings. This MP4 video was recorded at a talk before the International Center for Mathematical Sciences at the University of Edinburgh.

Intermittent criticality in financial markets: high frequency trading to large-scale bubbles and crashes. You have to download the file to play it.

By way of précis, this presentation offers a high-level summary of the roots of his approach in the economics literature, and highlights the role of a central differential equation for price change in an asset market.

So since I know everyone reading this blog was looking forward to learning about a differential equation, today, let me highlight the importance of the equation,

dp/dt = cpd

This basically says that price change in a market over time depends on the level of prices – a feature of markets where speculative forces begin to hold sway.

This looks to be a fairly simple equation, but the solutions vary, depending on the values of the parameters c and d. For example, when c>0 and the exponent d  is greater than one, prices change faster than exponentially and within some finite period, a singularity is indicated by the solution to the equation. Technically, in the language of differential equations this is called a finite time singularity.

Well, the essence of Sornette’s predictive approach is to estimate the parameters of a price equation that derives, ultimately, from this differential equation in order to predict when an asset market will reach its peak price and then collapse rapidly to lower prices.

The many sources of positive feedback in asset pricing markets are the basis for the faster than exponential growth, resulting from d>1. Lots of empirical evidence backs up the plausibility and credibility of herd and imitative behaviors, and models trace out the interaction of prices with traders motivated by market fundamentals and momentum traders or trend followers.

Interesting new research on this topic shows that random trades could moderate the rush towards collapse in asset markets – possibly offering an alternative to standard regulation.

The important thing, in my opinion, is to discard notions of market efficiency which, even today among some researchers, result in scoffing at the concept of asset bubbles and basic sabotage of research that can help understand the associated dynamics.

Here is a TED talk by Sornette from last summer.

financial forecasts, financial risk management, probability theory, tail events

Predicting Financial Crisis – the Interesting Case of Nassim Taleb

Note: This is good post from the old series, and I am re-publishing it with the new citation to Taleb’s book in progress Hidden Risk and a new video.

———————————————–

One of the biggest questions is whether financial crises can be predicted in any real sense. This is a major concern of mine. I was deep in the middle of forecasting on an applied basis during 2008-2010, and kept hoping to find proxies to indicate, for example, when we were coming out of it, or whether it would “double-dip.”

Currently, as noted in this blog, a chorus of voices (commentators, analysts, experts) says that all manner of asset bubbles are forming globally, beginning with the US stock and the Chinese real estate markets.

But does that mean that we can predict the timing of this economic and financial crisis, or are we all becoming “Chicken Littles?”

What we want is well-described by Mark Buchanan, when he writes

The challenge for economists is to find those indicators that can provide regulators with reliable early warnings of trouble. It’s a complicated task. Can we construct measures of asset bubbles, or devise ways to identify “too big to fail” or “too interconnected to fail” institutions? Can we identify the architectural features of financial networks that make them prone to cascades of distress? Can we strike the right balance between the transparency needed to make risks evident, and the privacy required for markets to function?

And, ah yes – there is light at the end of the tunnel –

Work is racing ahead. In the U.S., the newly formed Office of Financial Research has published various papers on topics such as stress tests and data gaps — including one that reviews a list of some 31 proposed systemic-risk measures. The economists John Geanakoplos and Lasse Pedersen have offered specific proposals on measuring the extent to which markets are driven by leverage, which tends to make the whole system more fragile.

The Office of Financial Research (OFR) in the Treasury Department was created by the Dodd-Frank legislation, and it is precisely here Nassim Taleb enters the picture, at a Congressional hearing on formation of the OFR.

   untitled

Mr. Chairman, Ranking Member, Members of the Committee, thank you for giving me the opportunity to testify on the analytical ambitions and centralized risk-management plans of Office of Financial Research (OFR). I am here primarily as a practitioner of risk —not as an analyst but as a decision-maker, an eyewitness of the poor, even disastrous translation of risk research into practice. I spent close to two decades as a derivatives trader before becoming a full-time scholar and researcher in the areas of risk and probability, so I travelled the road between theory and practice in the opposite direction of what is commonly done. Even when I was in full-time practice I specialized in errors linked to theories, and the blindness from the theories of risk management. Allow me to present my conclusions upfront and in no uncertain terms: this measure, if I read it well, aims at the creation of an omniscient Soviet-style central risk manager. It makes us fall into the naive illusion of risk management that got us here —the same illusion has led in the past to the blind accumulation of Black Swan risks. Black Swans are these large, consequential, but unpredicted deviations in the eyes of a given observer —the observer does not see them coming, but, by some mental mechanism, thinks that he predicted them. Simply, there are limitations to our ability to measure the risks of extreme events and throwing government money on it will carry negative side effects. 1) Financial risks, particularly those known as Black Swan events cannot be measured in any possible quantitative and predictive manner; they can only be dealt with nonpredictive ways.  The system needs to be made robust organically, not through centralized risk management. I will keep repeating that predicting financial risks has only worked on computers so far (not in the real world) and there is no compelling reason for that to change—as a matter of fact such class of risks is becoming more unpredictable

A reviewer in the Harvard Business Review notes Taleb is a conservative with a small c. But this does not mean that he is a toady for the Koch brothers or other special interests. In fact, in this Congressional testimony, Taleb also recommends, as his point #3

..risks need to be handled by the entities themselves, in an organic way, paying for their mistakes as they go. It is far more effective to make bankers accountable for their mistakes than try the central risk manager version of Soviet-style central planner, putting hope ahead of empirical reality.

Taleb’s argument has a mathematical side. In an article in the International Journal of Forecasting appended to his testimony, he develops infographics to suggest that fat-tailed risks are intrinsically hard to evaluate. He also notes, correctly, that in 2008, despite manifest proof to the contrary, leading financial institutions often applied risk models based on the idea that outcomes followed a normal or Gaussian probability distribution. It’s easy to show that this is not the case for daily stock and other returns. The characteristic distributions exhibit excess kurtosis, and are hard to pin down in terms of specific distributions. As Taleb points out, the defining events that might tip the identification one way or another are rare. So mistakes are easy to make, and possibly have big effects.

But, Taleb’s extraordinary talent for exposition is on full view in an recent article How To Prevent Another Financial Crisis, coauthored with George Martin. The first paragraphs give us the conclusion,

We believe that “less is more” in complex systems—that simple heuristics and protocols are necessary for complex problems as elaborate rules often lead to “multiplicative branching” of side effects that cumulatively may have first order effects. So instead of relying on thousands of meandering pages of regulation, we should enforce a basic principle of “skin in the game” when it comes to financial oversight: “The captain goes down with the ship; every captain and every ship.” In other words, nobody should be in a position to have the upside without sharing the downside, particularly when others may be harmed. While this principle seems simple, we have moved away from it in the finance world, particularly when it comes to financial organizations that have been deemed “too big to fail.”

Then, the authors drive this point home with a salient reference –

The best risk-management rule was formulated nearly 4,000 years ago. Hammurabi’s code specifies: “If a builder builds a house for a man and does not make its construction firm, and the house which he has built collapses and causes the death of the owner of the house, that builder shall be put to death.” Clearly, the Babylonians understood that the builder will always know more about the risks than the client, and can hide fragilities and improve his profitability by cutting corners—in, say, the foundation. The builder can also fool the inspector (or the regulator). The person hiding risk has a large informational advantage over the one looking for it.

My hat’s off to Taleb. A brilliant example, and the rest of the article bears reading too.

While I have not thrown in the towel when it comes to devising metrics to signal financial crisis, I have to say that thoughts like Taleb’s probability argument occurred to me recently, when considering the arguments over extreme weather events.

Here’s a recent video.