Tag Archives: accuracy of forecasts

accuracy of forecasts, Big Data, boosting, macroeconomic forecasting, time series forecasting, yield curve

Leading Indicators

June 2, 2014 Clive Jones

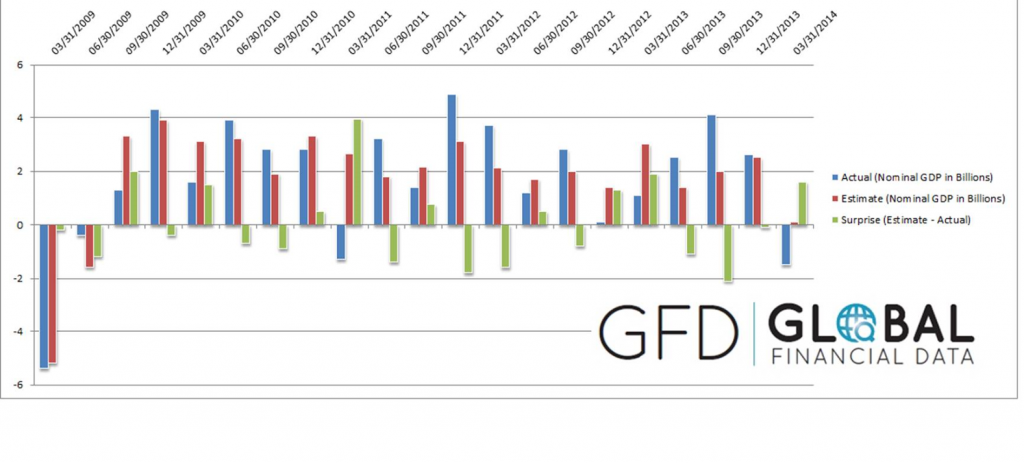
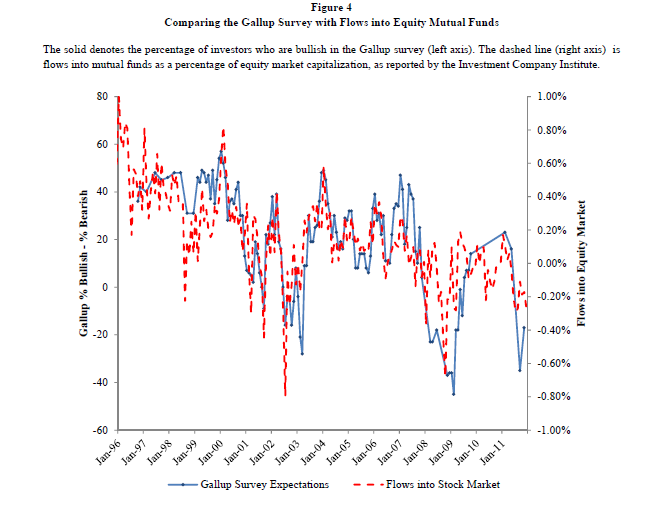
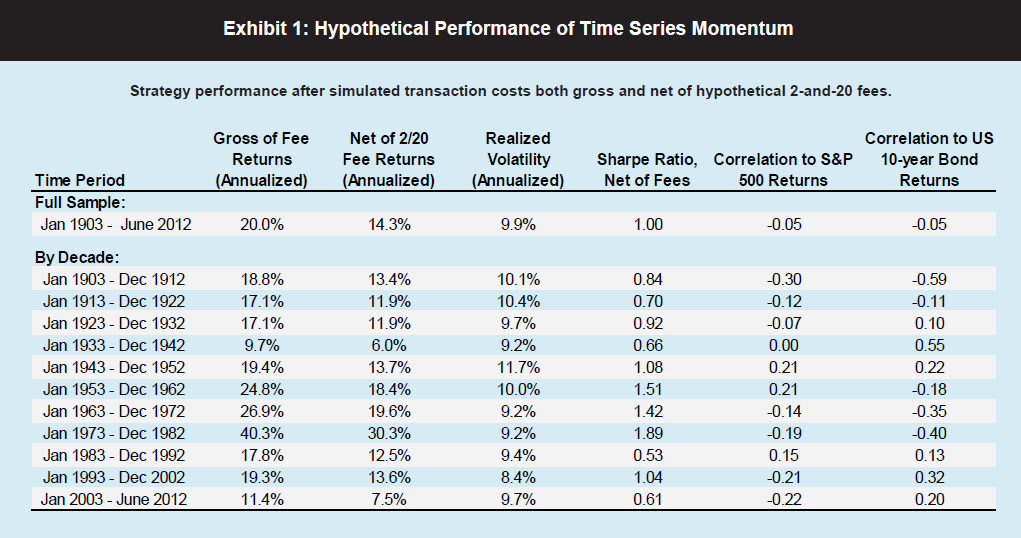
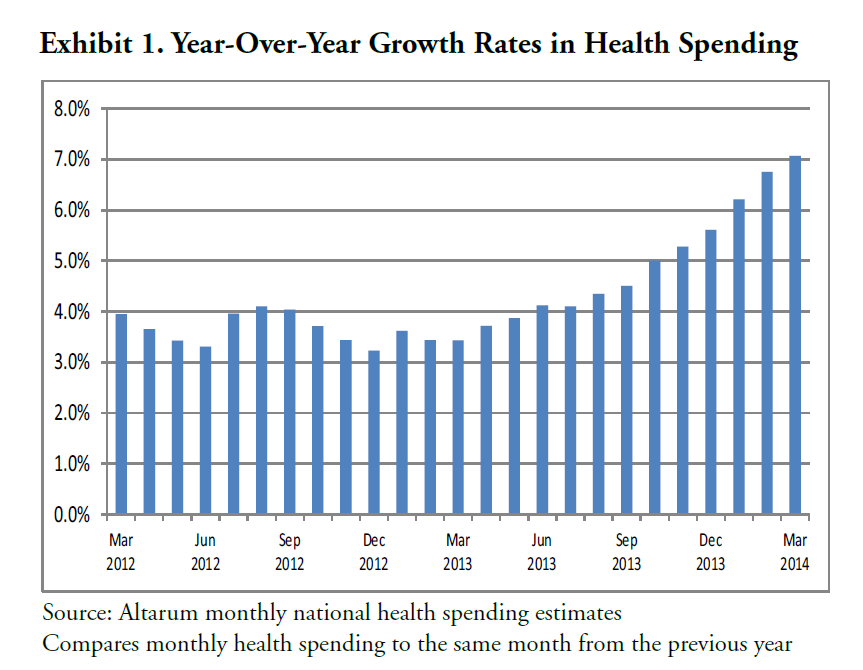
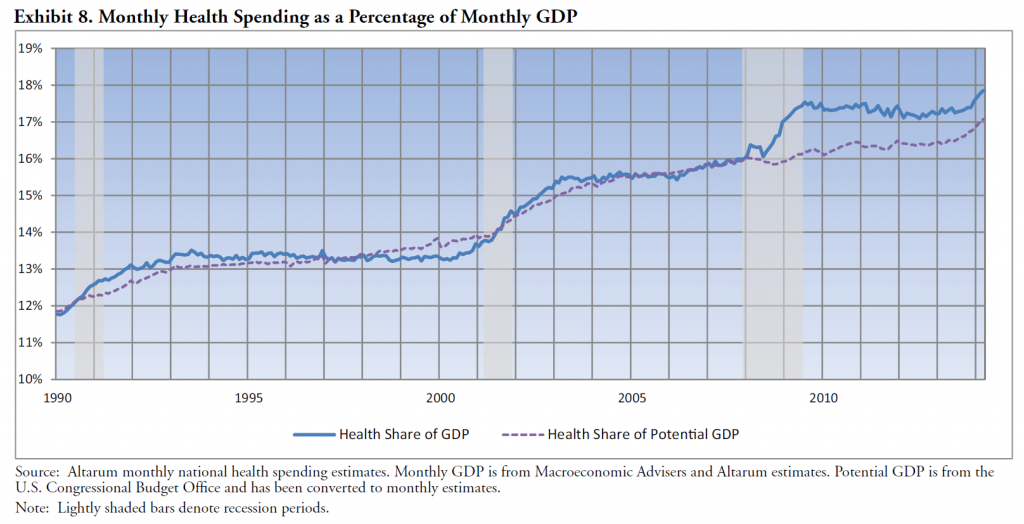
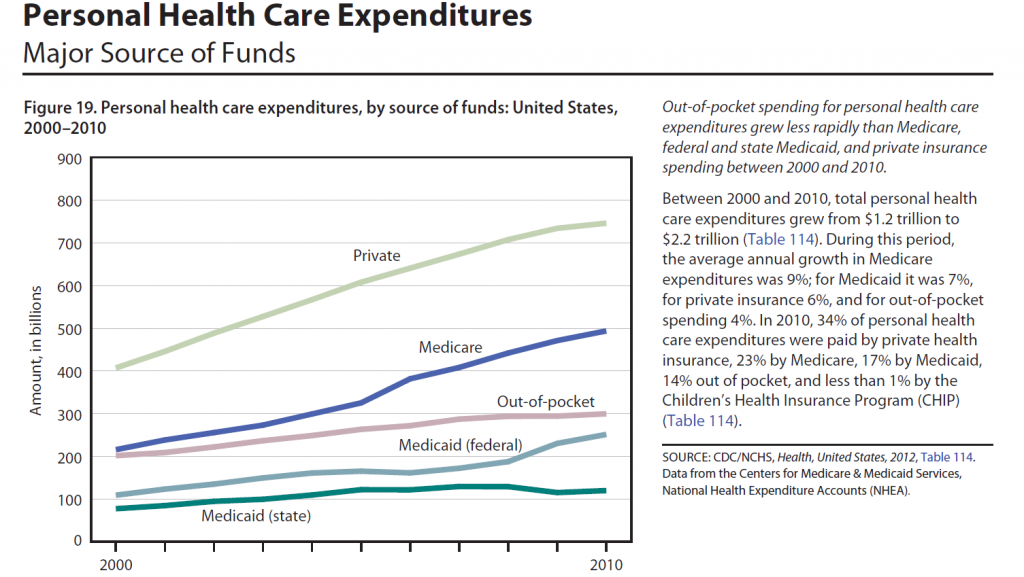
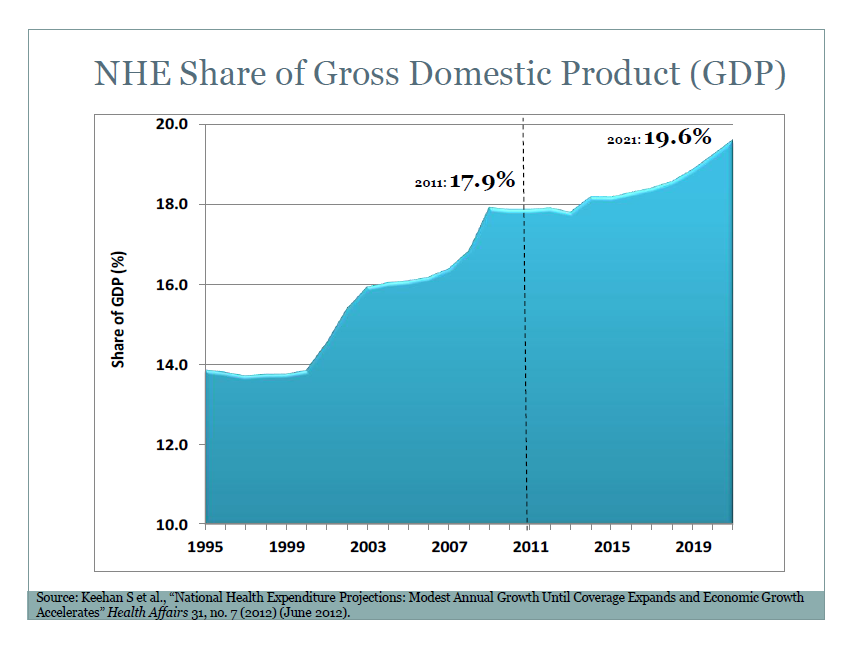
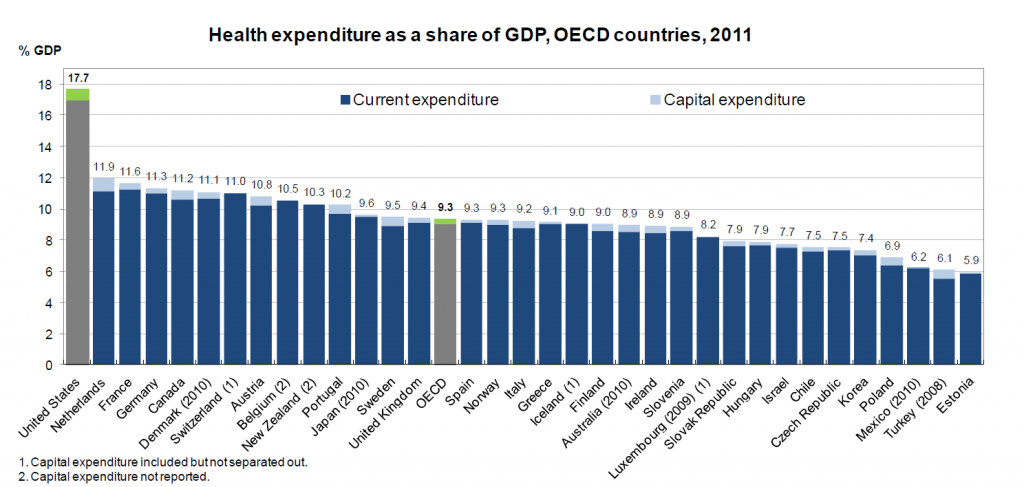
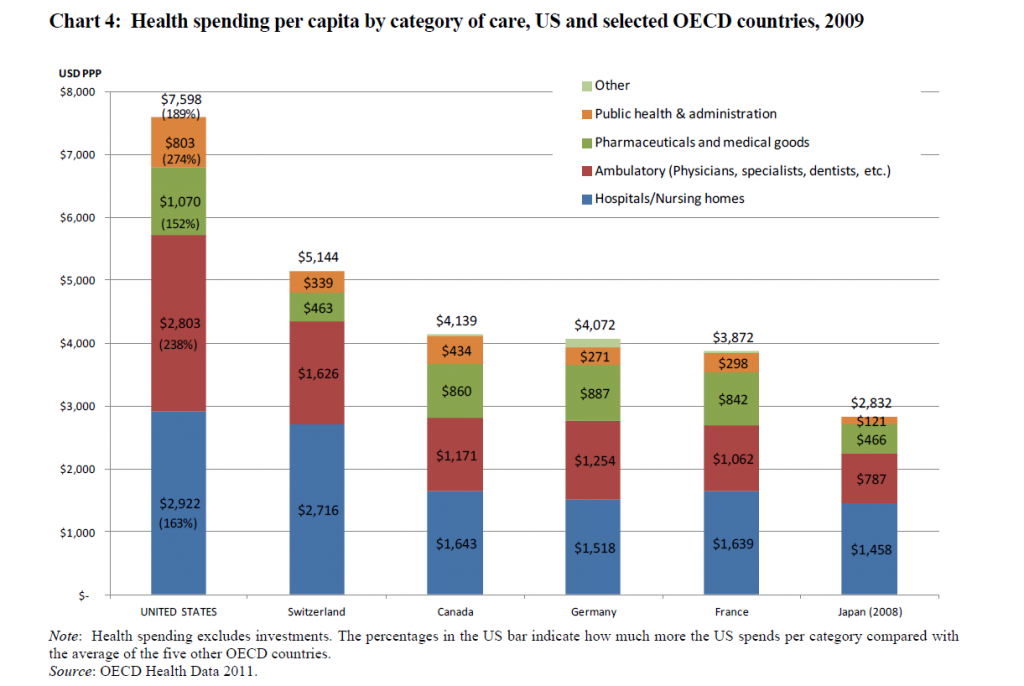
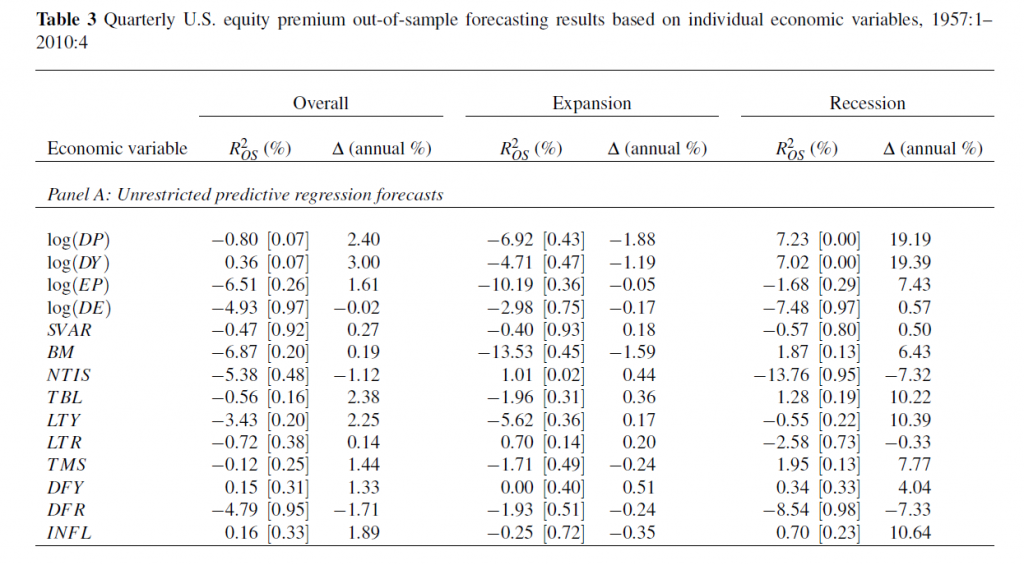
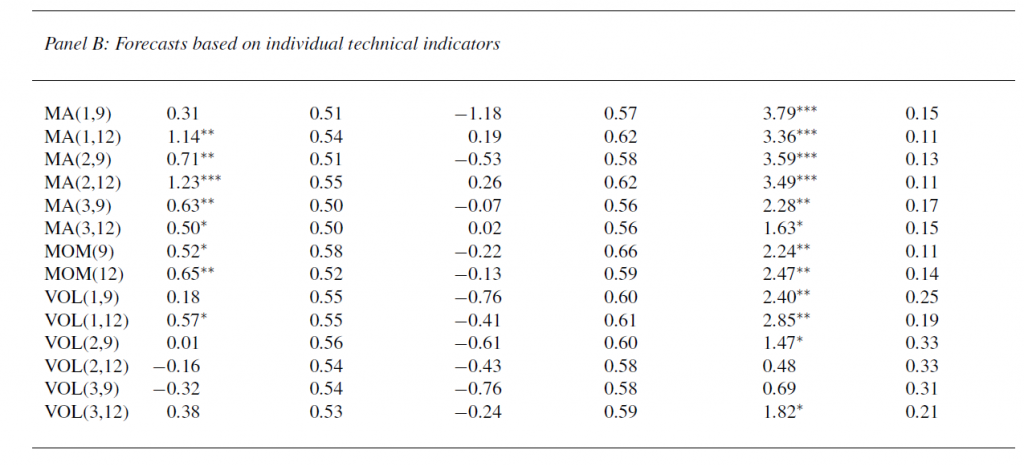
One value the forecasting community can provide is to report on the predictive power of various leading indicators for key economic and business series.

The Conference Board Leading Indicators

The Conference Board, a private, nonprofit organization with business membership, develops and publishes leading indicator indexes (LEI) for major national economies. Their involvement began in 1995, when they took over maintaining Business Cycle Indicators (BCI) from the US Department of Commerce.

For the United States, the index of leading indicators is based on ten variables: average weekly hours, manufacturing, average weekly initial claims for unemployment insurance, manufacturers’ new orders, consumer goods and materials, vendor performance, slower deliveries diffusion index,manufacturers’ new orders, nondefense capital goods, building permits, new private housing units, stock prices, 500 common stocks, money supply, interest rate spread, and an index of consumer expectations.

The Conference Board, of course, also maintains coincident and lagging indicators of the business cycle.

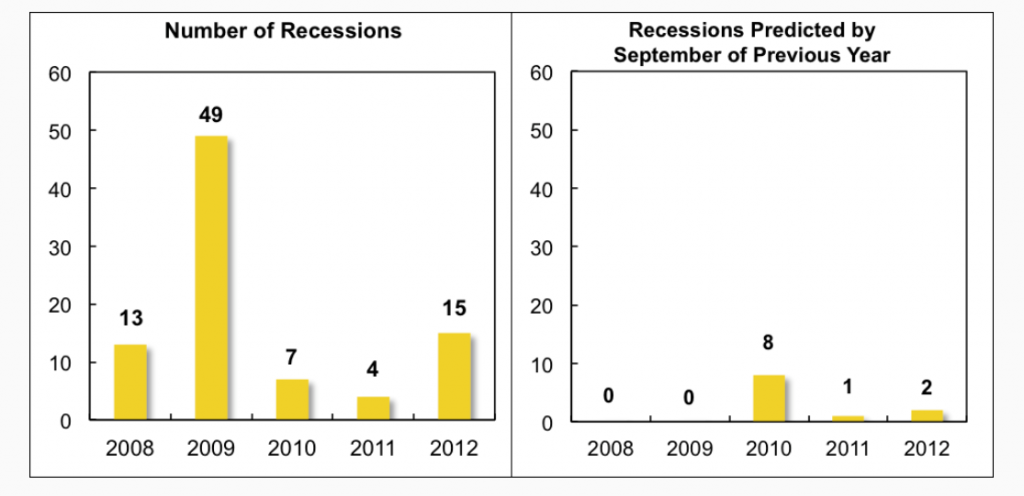
This list has been imprinted on the financial and business media mind, and is a convenient go-to, when a commentator wants to talk about what’s coming in the markets. And it used to be that a rule of thumb that three consecutive declines in the Index of Leading Indicators over three months signals a coming recession. This rule over-predicts, however, and obviously, given the track record of economists for the past several decades, these Conference Board leading indicators have questionable predictive power.

Serena Ng Research

What does work then?

Obviously, there is lots of research on this question, but, for my money, among the most comprehensive and coherent is that of Serena Ng, writing at times with various co-authors.

So in this regard, I recommend two recent papers

Boosting Recessions

Facts and Challenges from the Great Recession for Forecasting and Macroeconomic Modeling

The first paper is most recent, and is a talk presented before the Canadian Economic Association (State of the Art Lecture).

Hallmarks of a Serena Ng paper are coherent and often quite readable explanations of what you might call the Big Picture, coupled with ambitious and useful computation – usually reporting metrics of predictive accuracy.

Professor Ng and her co-researchers apparently have determined several important facts about predicting recessions and turning points in the business cycle.

For example –

Since World War II, and in particular, over the period from the 1970’s to the present, there have been different kinds of recessions. Following Ng and Wright, ..business cycles of the 1970s and early 80s are widely believed to be due to supply shocks and/or monetary policy. The three recessions since 1985, on the other hand, originate from the financial sector with the Great Recession of 2008-2009 being a full-blown balance sheet recession. A balance sheet recession involves, a sharp increase in leverage leaves the economy vulnerable to small shocks because, once asset prices begin to fall, financial institutions, firms, and households all attempt to deleverage. But with all agents trying to increase savings simultaneously, the economy loses demand, further lowering asset prices and frustrating the attempt to repair balance sheets. Financial institutions seek to deleverage, lowering the supply of credit. Households and firms seek to deleverage, lowering the demand for credit.
Examining a monthly panel of 132 macroeconomic and financial time series for the period 1960-2011, Ng and her co-researchers find that .. the predictor set with systematic and important predictive power consists of only 10 or so variables. It is reassuring that most variables in the list are already known to be useful, though some less obvious variables are also identified. The main finding is that there is substantial time variation in the size and composition of the relevant predictor set, and even the predictive power of term and risky spreads are recession specific. The full sample estimates and rolling regressions give confidence to the 5yr spread, the Aaa and CP spreads (relative to the Fed funds rate) as the best predictors of recessions.

So, the yield curve, a old favorite when it comes to forecasting recessions or turning points in the business cycle, performs less well in the contemporary context – although other (limited) research suggests that indicators combining facts about the yield curve with other metrics might be helpful.

And this exercise shows that the predictor set for various business cycles changes over time, although there are a few predictors that stand out. Again,

there are fewer than ten important predictors and the identity of these variables change with the forecast horizon. There is a distinct difference in the size and composition of the relevant predictor set before and after mid-1980. Rolling window estimation reveals that the importance of the term and default spreads are recession specific. The Aaa spread is the most robust predictor of recessions three and six months ahead, while the risky bond and 5yr spreads are important for twelve months ahead predictions. Certain employment variables have predictive power for the two most recent recessions when the interest rate spreads were uninformative. Warning signals for the post 1990 recessions have been sporadic and easy to miss.

Let me throw in my two bits here, before going on in subsequent posts to consider turning points in stock markets and in more micro-focused or industry time series.

At the end of “Boosting Recessions” Professor Ng suggests that higher frequency data may be a promising area for research in this field.

My guess is that is true, and that, more and more, Big Data and data analytics from machine learning will be applied to larger and more diverse sets of macroeconomics and business data, at various frequencies.

This is tough stuff, because more information is available today than in, say, the 1970’s or 1980’s. But I think we know what type of recession is coming – it is some type of bursting of the various global bubbles in stock markets, real estate, and possibly sovereign debt. So maybe more recent data will be highly relevant.

accuracy of forecasts, bias in forecasts, macroeconomic forecasting, predicting recessions, predicting turning points

“The Record of Failure to Predict Recessions is Virtually Unblemished”

June 1, 2014 Clive Jones

That’s Prakash Loungani from work published in 2001.

Recently, Loungani , working with Hites Ahir, put together an update – “Fail Again, Fail Better, Forecasts by Economists During the Great Recession” reprised in a short piece in VOX – “There will be growth in the spring”: How well do economists predict turning points?

Hites and Loungani looked at the record of professional forecasters 2008-2012. Defining recessions as a year-over-year fall in real GDP, there were 88 recessions in this period. Based on country-by-country predictions documented by Consensus Forecasts, economic forecasters were right less than 10 percent of the time, when it came to forecasting recessions – even a few months before their onset.

The chart on the left shows the timing of the 88 recession years, while the chart on the right shows the number of recession predicted by economists by the September of the previous year.

..none of the 62 recessions in 2008–09 was predicted as the previous year was drawing to a close. However, once the full realisation of the magnitude and breadth of the Great Recession became known, forecasters did predict by September 2009 that eight countries would be in recession in 2010, which turned out to be the right call in three of these cases. But the recessions in 2011–12 again came largely as a surprise to forecasters.

This type of result holds up to robustness checks

•First, lowering the bar on how far in advance the recession is predicted does not appreciably improve the ability to forecast turning points.

•Second, using a more precise definition of recessions based on quarterly data does not change the results.

•Third, the failure to predict turning points is not particular to the Great Recession but holds for earlier periods as well.

Forecasting Turning Points

How can macroeconomic and business forecasters consistently get it so wrong?

Well, the data is pretty bad, although there is more and more of it available and with greater time depths and higher frequencies. Typically, government agencies doing the national income accounts – the Bureau of Economic Analysis (BEA) in the United States – release macroeconomic information at one or two months lag (or more). And these releases usually involve revision, so there may be preliminary and then revised numbers.

And the general accuracy of GDP forecasts is pretty low, as Ralph Dillon of Global Financial Data (GFD) documents in the following chart, writing,

Below is a chart that has 5 years of quarterly GDP consensus estimates and actual GDP [for the US]. In addition, I have also shown in real dollars the surprise in both directions. The estimate vs actual with the surprise indicating just how wrong consensus was in that quarter.

Somehow, though, it is hard not to believe economists are doing something wrong with their almost total lack of success in predicting recessions. Perhaps there is a herding phenomenon, coupled with a distaste for being a bearer of bad tidings.

Or maybe economic theory itself plays a role. Indeed, earlier research published on Vox suggests that application of about 50 macroeconomic models to data preceding the recession of 2008-2009, leads to poor results in forecasting the downturn in those years, again even well into that period.

All this suggests economics is more or less at the point medicine was in the 1700’s, when bloodletting was all the rage..

In any case, this is the planned topic for several forthcoming posts, hopefully this coming week – forecasting turning points.

Note: The picture at the top of this post is Peter Sellers in his last role as Chauncey Gardiner – the simple-minded gardener who by an accident and stroke of luck was taken as a savant, and who said to the President – “There will be growth in the spring.”

accuracy of forecasts, cross-validation, multivariate modeling, predictive analytics, regression diagnostics

First Cut Modeling – All Possible Regressions

May 20, 2014 Clive Jones

If you can, form the regression

Y = β₀+ β₁X₁+ β₂X₂+…+ β_NX_N

where Y is the target variable and the N variagles X_i are the predictors which have the highest correlations with the target variables, based on some cutoff value of the correlation, say +/- 0.3.

Of course, if the number of observations you have in the data are less than N, you can’t estimate this OLS regression. Some “many predictors” data shrinkage or dimension reduction technique is then necessary – and will be covered in subsequent posts.

So, for this discussion, assume you have enough data to estimate the above regression.

Chances are that the accompanying measures of significance of the coefficients β_i– the t-statistics or standard errors – will indicate that only some of these betas are statistically significant.

And, if you poke around some, you probably will find that it is possible to add some of the predictors which showed low correlation with the target variable and have them be “statistically significant.”

So this is all very confusing. What to do?

Well, if the number of predictors is, say, on the order of 20, you can, with modern computing power, simply calculate all possible regressions with combinations of these 20 predictors. That turns out to be around 1 million regressions (2¹⁰ – 1). And you can reduce this number by enforcing known constraints on the betas, e.g. increasing family income should be unambiguously related to the target variable and, so, if its sign in a regression is reversed, throw that regression out from consideration.

The statistical programming language R has packages set up to do all possible regressions. See, for example, Quick-R which offers this useful suggestion –

But what other metrics, besides R², should be used to evaluate the possible regressions?

In-Sample Regression Metrics

I am not an authority on the Akaike Information Criterion (AIC) or the Bayesian Information Criterion (BIC), which, in addition, to good old R², are leading in-sample metrics for regression adequacy.

With this disclaimer, here are a few points about the AIC and BIC.

The AIC and BIC can be calculated with simple formulas.

So, as you can see, both the AIC and BIC are functions of the mean square error (MSE), as well as the number of predictors in the equation and the sample size. Both metrics essentially penalize models with a lot of explanatory variables, compared with other models that might perform similarly with fewer predictors.

There is something called the AIC-BIC dilemma. In a valuable reference on variable selection, Serena Ng writes that the AIC is understood to fall short when it comes to consistent model selection. Hyndman, in another must-read on this topic, writes that because of the heavier penalty, the model chosen by BIC is either the same as that chosen by AIC, or one with fewer terms.

Consistency in discussions of regression methods relates to the large sample properties of the metric or procedure in question. Basically, as the sample size n becomes indefinitely large (goes to infinity) consistent estimates or metrics converge to unbiased values. So the AIC is not in every case consistent, although I’ve read research which suggests that the problem only arises in very unusual setups.

In many applications, the AIC and BIC can both be minimum for a particular model, suggesting that this model should be given serious consideration.

Out-of-Sample Regression Metrics

I’m all about out-of-sample (OOS) metrics of adequacy of forecasting models.

It’s too easy to over-parameterize models and come up with good testing on in-sample data.

So I have been impressed with endorsements such as that of Hal Varian of cross-validation.

So, ideally, you partition the sample data into training and test samples. You estimate the predictive model on the training sample, and then calculate various metrics of adequacy on the test sample.

The problem is that often you can’t really afford to give up that much data to the test sample.

So cross-validation is one solution.

In k-fold cross validation, you partition the sample into k parts, estimating the designated regression on data from k-1 of those segments, and using the other or kth segment to test the model. Do this k times and then average or somehow collate the various error metrics. That’s the drill.,

Again, Quick-R suggests useful R code.

Hyndman also highlights a handy matrix formula to quickly compute the Leave Out One Cross Validation (LOOCV) metric.

LOOCV is not guaranteed to find the true model as the sample size increases, i.e. it is not consistent.

However, k-fold cross-validation can be consistent, if k increases with sample size.

Researchers recently have shown, however, that LOOCV can be consistent for the LASSO.

Selecting regression variables is, indeed, a big topic.

Coming posts will focus on the problem of “many predictors” when the set of predictors is greater in number than the set of observations on the relevant variables.

Selecting Predictors

May 18, 2014 Clive Jones

In a recent post on logistic regression, I mentioned research which developed diagnostic tools for breast cancer based on true Big Data parameters – notably 62,219 consecutive mammography records from 48,744 studies in 18,270 patients reported using the Breast Imaging Reporting and Data System (BI-RADS) lexicon and the National Mammography Database format between April 5, 1999 and February 9, 2004.

This research built a logistic regression model with 36 predictors, selected from the following information residing in the National Mammography Database (click to enlarge).

The question arises – are all these 36 predictors significant? Or what is the optimal model? How does one select the subset of the available predictor variables which really count?

This is the problem of selecting predictors in multivariate analysis – my focus for several posts coming up.

So we have a target variable y and set of potential predictors x={x1,x2,….,xn}. We are interested in discovering a predictive relationship, y=F(x^*) where x^* is some possibly proper subset of x. Furthermore, we have data comprising m observations on y and x, which in due time we will label with subscripts.

There are a range of solutions to this very real, very practical modeling problem.

Here is my short list.

Forward Selection. Begin with no candidate variables in the model. Select the variable that boosts some goodness-of-fit or predictive metric the most. Traditionally, this has been R-Squared for an in-sample fit. At each step, select the candidate variable that increases the metric the most. Stop adding variables when none of the remaining variables are significant. Note that once a variable enters the model, it cannot be deleted.
Backward Selection. This starts with the superset of potential predictors and eliminates variables which have the lowest score by some metric – traditionally, the t-statistic.
Stepwise regression. This combines backward and forward selection of regressors.
Regularization and Selection by means of the LASSO. Here is the classic article and here is a post, and here is a post in this blog on the LASSO.
Information criteria applied to all possible regressions – pick the best specification by applying the Aikaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) to all possible combinations of regressors. Clearly, this is only possible with a limited number of potential predictors.
Cross-validation or other out-of-sample criteria applied to all possible regressions – Typically, the error metrics on the out-of-sample data cuts are averaged, and the lowest average error model is selected out of all possible combinations of predictors.
Dimension reduction or data shrinkage with principal components. This is a many predictors formulation, whereby it is possible to reduce a large number of predictors to a few principal components which explain most of the variation in the data matrix.
Dimension reduction or data shrinkage with partial least squares. This is similar to the PC approach, but employs a reduction to information from both the set of potential predictors and the dependent or target variable.

There certainly are other candidate techniques, but this is a good list to start with.

Wonderful topic, incidentally. Dives right into the inner sanctum of the mysteries of statistical science as practiced in the real world.

Let me give you the flavor of how hard it is to satisfy the classical criterion for variable selection, arriving at unbiased or consistent estimates of effects of a set of predictors.

And, really, the paradigmatic model is ordinary least squares (OLS) regression in which the predictive function F(.) is linear.

The Specification Problem

The problem few analysts understand is called specification error.

So assume that there is a true model – some linear expression in variables multiplied by their coefficients, possibly with a constant term added.

Then, we have some data to estimate this model.

Now the specification problem is that when predictors are not orthogonal, i.e. when they are correlated, leaving out a variable from the “true” specification imparts a bias to the estimates of coefficients of variables included in the regression.

This complications sequential methods of selecting predictors for the regression.

So in any case I will have comments forthcoming on methods of selecting predictors.

accuracy of forecasts, stock market forecasts

Trend Following in the Stock Market

May 16, 2014 Clive Jones

Noah Smith highlights some amazing research on investor attitudes and behavior in Does trend-chasing explain financial markets?

He cites 2012 research by Greenwood and Schleifer where these researchers consider correlations between investor expectations, as measured by actual investor surveys, and subsequent investor behavior.

A key graphic is the following:

This graph shows rather amazingly, as Smith points out..when people say they expect stocks to do well, they actually put money into stocks. How do you find out what investor expectations are? – You ask them – then it’s interesting it’s possible to show that for the most part they follow up attitudes with action.

This discussion caught my eye since Sornette and others attribute the emergence of bubbles to momentum investing or trend-following behavior. Sometimes Sornette reduces this to “herding” or mimicry. I think there are simulation models, combining trend investors with others following a market strategy based on “fundamentals”, which exhibit cumulating and collapsing bubbles.

More on that later, when I track all that down.

For the moment, some research put out by AQR Capital Management in Greenwich CT makes big claims for an investment strategy based on trend following –

The most basic trend-following strategy is time series momentum – going long markets with recent positive returns and shorting those with recent negative returns. Time series momentum has been profitable on average since 1985 for nearly all equity index futures, fixed income futures, commodity futures, and currency forwards. The strategy explains the strong performance of Managed Futures funds from the late 1980s, when fund returns and index data first becomes available.

This paragraph references research by Moscowitz and Pederson published in the Journal of Financial Economics – an article called Time Series Momentum.

But more spectacularly, this AQR white paper presents this table of results for a trend-following investment strategy decade-by-decade.

There are caveats to this rather earth-shaking finding, but what it really amounts to for many investors is a recommendation to look into managed futures.

Along those lines there is this video interview, conducted in 2013, with Brian Hurst, one of the authors of the AQR white paper. He reports that recently trending-following investing has run up against “choppy” markets, but holds out hope for the longer term –

http://www.morningstar.com/advisor/v/69423366/will-trends-reverse-for-managed-futures.htm

At the same time, caveat emptor. Bloomberg reported late last year that a lot of investors plunging into managed futures after the Great Recession of 2008-2009 have been disappointed, in many cases, because of the high, unregulated fees and commissions involved in this type of alternative investment.

accuracy of forecasts, forecasting medical and healthcare costs, Medical data analytics

Forecasts in the Medical and Health Care Fields

May 13, 2014 Clive Jones

I’m focusing on forecasting issues in the medical field and health care for the next few posts.

One major issue is the cost of health care in the United States and future health care spending. Just when many commentators came to believe the growth in health care expenditures was settling down to a more moderate growth path, spending exploded in late 2013 and in the first quarter of 2014, growing at a year-over-year rate of 7 percent (or higher, depending on how you cut the numbers). Indeed, preliminary estimates of first quarter GDP growth would have been negative– indicating start of a possible new recession – were it not for the surge in healthcare spending.

Annualizing March 2014 numbers, US health case spending is now on track to hit a total of $3.07 trillion.

Here are estimates of month-by-month spending from the Altarum Institute.

The Altarum Institute blends data from several sources to generate this data, and also compiles information showing how medical spending has risen in reference to nominal and potential GDP.

Payments from Medicare and Medicaid have been accelerating, as the following chart from the comprehensive Center for
Disease Control (CDC) report suggests.

Projections of Health Care Spending

One of the primary forecasts in this field is the Centers for Medicare & Medicaid Services’ (CMS) National Health Expenditures (NHE) projections.

The latest CMS projections have health spending projected to grow at an average rate of 5.8 percent from 2012-2022, a percentage point faster than expected growth in nominal GDP.

The Affordable Care Act is one of the major reasons why health care spending is surging, as millions who were previously not covered by health insurance join insurance exchanges.

The effects of the ACA, as well as continued aging of the US population and entry of new and expensive medical technologies, are anticipated to boost health care spending to 19-20 percent of GDP by 2021.

The late Robert Fogel put together a projection for the National Bureau of Economic Research (NBER) which suggested the ratio of health care spending to GDP would rise to 29 percent by 2040.

The US Health Care System Is More Expensive Than Others

I get the feeling that the econometric and forecasting models for these extrapolations – as well as the strategically important forecasts for future Medicare and Medicaid costs – are sort of gnarly, compared to the bright shiny things which could be developed with the latest predictive analytics and Big Data methods.

Neverhteless, it is interesting that an accuracy analysis of the CMS 11 year projections shows them to be are relatively good, at least one to three years out from current estimates. That was, of course, over a period with slowing growth.

But before considering any forecasting model in detail, I think it is advisable to note how anomalous the US health care system is in reference to other (highly developed) countries.

The OECD, for example, develops
interesting comparisons of medical spending in the US and other developed and emerging economies.

The OECD data also supports a breakout of costs per capita, as follows.

So the basic reason why the US health care system is so expensive is that, for example, administrative costs per capita are more than double those in other developed countries. Practitioners also are paid almost double that per capital of what they receive in these other countries, countries with highly regarded healthcare systems. And so forth and so on.

The Bottom Line

Health care costs in the US typically grow faster than GDP, and are expected to accelerate for the rest of this decade. The ratio of health care costs to US GDP is rising, and longer range forecasts suggest almost a third of all productive activity by mid-century will be in health care and the medical field.

This suggests either a radically different type of society – a care-giving culture, if you will – or that something is going to break or make a major transition between now and then.

accuracy of forecasts, financial forecasting, partial least squares, stock market forecasts, three pass regression filter (3PRF)

Looking Ahead, Looking Back

May 10, 2014 Clive Jones

Looking ahead, I’m almost sure I want to explore forecasting in the medical field this coming week. Menzie Chin at Econbrowser, for example, highlights forecasts that suggest states opting out of expanded Medicare are flirting with higher death rates. This sets off a flurry of comments, highlighting the importance and controversy attached to various forecasts in the field of medical practice.

There’s a lot more – from bizarre and sad mortality trends among Russian men since the collapse of the Soviet Union, now stabilizing to an extent, to systems which forecast epidemics, to, again, cost and utilization forecasts.

Today, however, I want to wind up this phase of posts on forecasting the stock and related financial asset markets.

Market Expectations in the Cross Section of Present Values

That’s the title of Bryan Kelly and Seth Pruitt’s article in the Journal of Finance, downloadable from the Social Science Research Network (SSRN).

The following chart from this paper shows in-sample (IS) and out-of-sample (OOS) performance of Kelly and Pruitt’s new partial least squares (PLS) predictor, and IS and OOS forecasts from another model based on the aggregate book-to-market ratio. (Click to enlarge)

The Kelly-Pruitt PLS predictor is much better in both in-sample and out-of-sample than the more traditional regression model based on aggregate book-t0-market ratios.

What Kelly and Pruitt do is use what I would call cross-sectional time series data to estimate aggregate market returns.

Basically, they construct a single factor which they use to predict aggregate market returns from cross-sections of portfolio-level book-to-market ratios.

So,

To harness disaggregated information we represent the cross section of asset-specific book-to-market ratios as a dynamic latent factor model. We relate these disaggregated value ratios to aggregate expected market returns and cash flow growth. Our model highlights the idea that the same dynamic state variables driving aggregate expectations also govern the dynamics of the entire panel of asset-specific valuation ratios. This representation allows us to exploit rich cross-sectional information to extract precise estimates of market expectations.

This cross-sectional data presents a “many predictors” type of estimation problem, and the authors write that,

Our solution is to use partial least squares (PLS, Wold (1975)), which is a simple regression-based procedure designed to parsimoniously forecast a single time series using a large panel of predictors. We use it to construct a univariate forecaster for market returns (or dividend growth) that is a linear combination of assets’ valuation ratios. The weight of each asset in this linear combination is based on the covariance of its value ratio with the forecast target.

I think it is important to add that the authors extensively explore PLS as a procedure which can be considered to be built from a series of cross-cutting regressions, as it were (See their white paper on three-pass regression filter).

But, it must be added, this PLS procedure can be summarized in a single matrix formula, which is

Readers wanting definitions of these matrices should consult the Journal of Finance article and/or the white paper mentioned above.

The Kelly-Pruitt analysis works where other methods essentially fail – in OOS prediction,

Using data from 1930-2010, PLS forecasts based on the cross section of portfolio-level book-to-market ratios achieve an out-of-sample predictive R2 as high as 13.1% for annual market returns and 0.9% for monthly returns (in-sample R2 of 18.1% and 2.4%, respectively). Since we construct a single factor from the cross section, our results can be directly compared with univariate forecasts from the many alternative predictors that have been considered in the literature. In contrast to our results, previously studied predictors typically perform well in-sample but become insignifcant out-of-sample, often performing worse than forecasts based on the historical mean return …

So, the bottom line is that aggregate stock market returns are predictable from a common-sense perspective, without recourse to abstruse error measures. And I believe Amit Goyal, whose earlier article with Welch contests market predictability, now agrees (personal communication) that this application of a PLS estimator breaks new ground out-of-sample – even though its complexity asks quite a bit from the data.

Note, though, how volatile aggregate realized returns for the US stock market are, and how forecast errors of the Kelly-Pruitt analysis become huge during the 2008-2009 recession and some previous recessions – indicated by the shaded lines in the above figure.

Still something is better than nothing, and I look for improvements to this approach – which already has been applied to international stocks by Kelly and Pruitt and other slices portfolio data.

accuracy of forecasts, financial forecasting, forecasting corporate bond returns, three pass regression filter (3PRF), time series forecasting

More on the Predictability of Stock and Bond Markets

May 6, 2014 Clive Jones

Research by Lin, Wu, and Zhou in Predictability of Corporate Bond Returns: A Comprehensive Study suggests a radical change in perspective, based on new forecasting methods. The research seems to me to of a piece with a lot of developments in Big Data and the data mining movement generally. Gains in predictability are associated with more extensive databases and new techniques.

The abstract to their white paper, presented at various conferences and colloquia, is straight-forward –

Using a comprehensive data set, we find that corporate bond returns not only remain predictable by traditional predictors (dividend yields, default, term spreads and issuer quality) but also strongly predictable by a new predictor formed by an array of 26 macroeconomic, stock and bond predictors. Results strongly suggest that macroeconomic and stock market variables contain important information for expected corporate bond returns. The predictability of returns is of both statistical and economic significance, and is robust to different ratings and maturities.

Now, in a way, the basic message of the predictability of corporate bond returns is not news, since Fama and French made this claim back in 1989 – namely that default and term spreads can predict corporate bond returns both in and out of sample.

What is new is the data employed in the Lin, Wu, and Zhou (LWZ) research. According to the authors, it involves 780,985 monthly observations spanning from January 1973 to June 2012 from combined data sources, including Lehman Brothers Fixed Income (LBFI), Datastream, National Association of Insurance Commissioners (NAIC), Trade Reporting and Compliance Engine (TRACE) and Mergents Fixed Investment Securities Database (FISD).

There also is a new predictor which LWZ characterize as a type of partial least squares (PLS) formulation, but which is none other than the three pass regression filter discussed in a post here in March.

The power of this PLS formulation is evident in a table showing out-of-sample R² of the various modeling setups. As in the research discussed in a recent post, out-of-sample (OS) R2 is a ratio which measures the improvement in mean square prediction errors (MSPE) for the predictive regression model over the historical average forecast. A negative OS R2 thus means that the MSPE of the benchmark forecast is less than the MSPE of the forecast by the designated predictor formulation.

Again, this research finds predictability varies with economic conditions – and is higher during economic downturns.

There are cross-cutting and linked studies here, often with Goyal’s data and fourteen financial/macroeconomic variables figuring within the estimations. There also is significant linkage with researchers at regional Federal Reserve Banks.

My purpose in this and probably the next one or two posts is to just get this information out, so we can see the larger outlines of what is being done and suggested.

My guess is that the sum total of this research is going to essentially re-write financial economics and has huge implications for forecasting operations within large companies and especially financial institutions.

accuracy of forecasts, ensemble forecasts, financial forecasting, forecasting research, stock market forecasts, time series forecasting

Stock Market Predictability – Controversy

May 5, 2014 Clive Jones

In the previous post, I drew from papers by Neeley, who is Vice President of the Federal Reserve Bank of St. Louis, David Rapach at St. Louis University and Goufu Zhou at Washington University in St. Louis.

These authors contribute two papers on the predictability of equity returns.

The earlier one – Forecasting the Equity Risk Premium: The Role of Technical Indicators – is coming out in Management Science. Of course, the survey article – Forecasting the Equity Risk Premium: The Role of Technical Indicators – is a chapter in the recent volume 2 of the Handbook of Forecasting.

I go through this rather laborious set of citations because it turns out that there is an underlying paper which provides the data for the research of these authors, but which comes to precisely the opposite conclusion –

The goal of our own article is to comprehensively re-examine the empirical evidence as of early 2006, evaluating each variable using the same methods (mostly, but not only, in linear models), time-periods, and estimation frequencies. The evidence suggests that most models are unstable or even spurious. Most models are no longer significant even insample (IS), and the few models that still are usually fail simple regression diagnostics.Most models have performed poorly for over 30 years IS. For many models, any earlier apparent statistical significance was often based exclusively on years up to and especially on the years of the Oil Shock of 1973–1975. Most models have poor out-of-sample (OOS) performance, but not in a way that merely suggests lower power than IS tests. They predict poorly late in the sample, not early in the sample. (For many variables, we have difficulty finding robust statistical significance even when they are examined only during their most favorable contiguous OOS sub-period.) Finally, the OOS performance is not only a useful model diagnostic for the IS regressions but also interesting in itself for an investor who had sought to use these models for market-timing. Our evidence suggests that the models would not have helped such an investor. Therefore, although it is possible to search for, to occasionally stumble upon, and then to defend some seemingly statistically significant models, we interpret our results to suggest that a healthy skepticism is appropriate when it comes to predicting the equity premium, at least as of early 2006. The models do not seem robust.

This is from Ivo Welch and Amit Goyal’s 2008 article A Comprehensive Look at The Empirical Performance of Equity Premium Prediction in the Review of Financial Studies which apparently won an award from that journal as the best paper for the year.

And, very importantly, the data for this whole discussion is available, with updates, from Amit Goyal’s site now at the University of Lausanne.

Where This Is Going

Currently, for me, this seems like a genuine controversy in the forecasting literature. And, as an aside, in writing this blog I’ve entertained the notion that maybe I am on the edge of a new form of or focus in journalism – namely stories about forecasting controversies. It’s kind of wonkish, but the issues can be really, really important.

I also have a “hands-on” philosophy, when it comes to this sort of information. I much rather explore actual data and run my own estimates, than pick through theoretical arguments.

So anyway, given that Goyal generously provides updated versions of the data series he and Welch originally used in their Review of Financial Studies article, there should be some opportunity to check this whole matter. After all, the estimation issues are not very difficult, insofar as the first level of argument relates primarily to the efficacy of simple bivariate regressions.

By the way, it’s really cool data.

Here is the book-to-market ratio, dating back to 1926.

But beyond these simple regressions that form a large part of the argument, there is another claim made by Neeley, Rapach, and Zhou which I take very seriously. And this is that – while a “kitchen sink” model with all, say, fourteen so-called macroeconomic variables does not outperform the benchmark, a principal components regression does.

This sounds really plausible.

Anyway, if readers have flagged updates to this controversy about the predictability of stock market returns, let me know. In addition to grubbing around with the data, I am searching for additional analysis of this point.

accuracy of forecasts, financial forecasting, predictive analytics, predictive performance of technical indicators of stock price, stock market forecasts

Evidence of Stock Market Predictability

May 4, 2014 Clive Jones

In business forecast applications, I often have been asked, “why don’t you forecast the stock market?” It’s almost a variant of “if you’re so smart, why aren’t you rich?” I usually respond something about stock prices being largely random walks.

But, stock market predictability is really the nut kernel of forecasting, isn’t it?

Earlier this year, I looked at the S&P 500 index and the SPY ETF numbers, and found I could beat a buy and hold strategy with a regression forecasting model. This was an autoregressive model with lots of lagged values of daily S&P returns. In some variants, it included lagged values of the Chicago Board of Trade VIX volatility index returns. My portfolio gains were compiled over an out-of-sample (OS) period. This means, of course, that I estimated the predictive regression on historical data that preceded and did not include the OS or test data.

Well, today I’m here to report to you that it looks like it is officially possible to achieve some predictability of stock market returns in out-of-sample data.

One authoritative source is Forecasting Stock Returns, an outstanding review by Rapach and Zhou in the recent, second volume of the Handbook of Economic Forecasting.

The story is fascinating.

For one thing, most of the successful models achieve their best performance – in terms of beating market averages or other common benchmarks – during recessions.

And it appears that technical market indicators, such as the oscillators, momentum, and volume metrics so common in stock trading sites, have predictive value. So do a range of macroeconomic indicators.

But these two classes of predictors – technical market and macroeconomic indicators – are roughly complementary in their performance through the business cycle. As Christopher Neeley et al detail in Forecasting the Equity Risk Premium: The Role of Technical Indicators,

Macroeconomic variables typically fail to detect the decline in the actual equity risk premium early in recessions, but generally do detect the increase in the actual equity risk premium late in recessions. Technical indicators exhibit the opposite pattern: they pick up the decline in the actual premium early in recessions, but fail to match the unusually high premium late in recessions.

Stock Market Predictors – Macroeconomic and Technical Indicators

Rapach and Zhou highlight fourteen macroeconomic predictors popular in the finance literature.

1. Log dividend-price ratio (DP): log of a 12-month moving sum of dividends paid on the S&P 500 index minus the log of stock prices (S&P 500 index).

2. Log dividend yield (DY): log of a 12-month moving sum of dividends minus the log of lagged stock prices.

3. Log earnings-price ratio (EP): log of a 12-month moving sum of earnings on the S&P 500 index minus the log of stock prices.

4. Log dividend-payout ratio (DE): log of a 12-month moving sum of dividends minus the log of a 12-month moving sum of earnings.

5. Stock variance (SVAR): monthly sum of squared daily returns on the S&P 500 index.

6. Book-to-market ratio (BM): book-to-market value ratio for the DJIA.

7. Net equity expansion (NTIS): ratio of a 12-month moving sum of net equity issues by NYSE-listed stocks to the total end-of-year market capitalization of NYSE stocks.

8. Treasury bill rate (TBL): interest rate on a three-month Treasury bill (secondary market).

9. Long-term yield (LTY): long-term government bond yield.

10. Long-term return (LTR): return on long-term government bonds.

11. Term spread (TMS): long-term yield minus the Treasury bill rate.

12. Default yield spread (DFY): difference between BAA- and AAA-rated corporate bond yields.

13. Default return spread (DFR): long-term corporate bond return minus the long-term government bond return.

14. Inflation (INFL): calculated from the CPI (all urban consumers

In addition, there are technical indicators, which are generally moving average, momentum, or volume-based.

The moving average indicators typically provide a buy or sell signal based on a comparing two moving averages – a short and a long period MA.

Momentum based rules are based on the time trajectory of prices. A current stock price higher than its level some number of periods ago indicates “positive” momentum and expected excess returns, and generates a buy signal.

Momentum rules can be combined with information about the volume of stock purchases, such as Granville’s on-balance volume.

Each of these predictors can be mapped onto equity premium excess returns – measured by the rate of return on the S&P 500 index net of return on a risk-free asset. This mapping is a simple bi-variate regression with equity returns from time t on the left side of the equation and the economic predictor lagged by one time period on the right side of the equation. Monthly data are used from 1927 to 2008. The out-of-sample (OS) period is extensive, dating from the 1950’s, and includes most of the post-war recessions.

The following table shows what the authors call out-of-sample (OS) R² for the 14 so-called macroeconomic variables, based on a table in the Handbook of Forecasting chapter. The OS R² is equal to 1 minus a ratio. This ratio has the mean square forecast error (MSFE) of the predictor forecast in the numerator and the MSFE of the forecast based on historic average equity returns in the denominator. So if the economic indicator functions to improve the OS forecast of equity returns, the OS R² is positive. If, on the other hand, the historic average trumps the economic indicator forecast, the OS R² is negative.

(click to enlarge).

Overall, most of the macro predictors in this list don’t make it. Thus, 12 of the 14 OS R² statistics are negative in the second column of the Table, indicating that the predictive regression forecast has a higher MSFE than the historical average.

For two of the predictors with a positive out-of-sample R², the p-values reported in the brackets are greater than 0.10, so that these predictors do not display statistically significant out-of-sample performance at conventional levels.

Thus, the first two columns in this table, under “Overall”, support a skeptical view of the predictability of equity returns.

However, during recessions, the situation is different.

For several the predictors, the R² OS statistics move from being negative (and typically below -1%) during expansions to 1% or above during recessions. Furthermore, some of these R² OS statistics are significant at conventional levels during recessions according to the p-values, despite the decreased number of available observations.

Now imposing restrictions on the regression coefficients substantially improves this forecast performance, as the lower panel (not shown) in this table shows.

Rapach and Zhou were coauthors of the study with Neeley, published earlier as a working paper with the St. Louis Federal Reserve.

This working paper is where we get the interesting report about how technical factors add to the predictability of equity returns (again, click to enlarge).

This table has the same headings for the columns as Table 3 above.

It shows out-of-sample forecasting results for several technical indicators, using basically the same dataset, for the overall OS period, for expansions, and recessions in this period dating from the 1950’s to 2008.

In fact, these technical indicators generally seem to do better than the 14 macroeconomic indicators.

Low OS R²

Even when these models perform their best, their increase in mean square forecast error (MSFE) is only slightly more than the MSFE of the benchmark historic average return estimate.

This improved performance, however, can still achieve portfolio gains for investors, based on various trading rules, and, as both papers point out, investors can use the information in these forecasts to balance their portfolios, even when the underlying forecast equations are not statistically significant by conventional standards. Interesting argument, and I need to review it further to fully understand it.

In any case, my experience with an autoregressive model for the S&P 500 is that trading rules can be devised which produce portfolio gains over a buy and hold strategy, even when the R²is on the order of 1 or a few percent. All you have to do is correctly predict the sign of the return on the following trading day, for instance, and doing this a little more than 50 percent of the time produces profits.

Rapach and Zhou, in fact, develop insights into how predictability of stock returns can be consistent with rational expectations – providing the relevant improvements in predictability are bounded to be low enough.

Some Thoughts

There is lots more to say about this, naturally. And I hope to have further comments here soon.

But, for the time being, I have one question.

The is why econometricians of the caliber of Rapach, Zhou, and Neeley persist in relying on tests of statistical significance which are predicated, in a strict sense, on the normality of the residuals of these financial return regressions.

I’ve looked at this some, and it seems the t-statistic is somewhat robust to violations of normality of the underlying error distribution of the regression. However, residuals of a regression on equity rates of return can be very non-normal with fat tails and generally some skewness. I keep wondering whether anyone has really looked at how this translates into tests of statistical significance, or whether what we see on this topic is mostly arm-waving.

For my money, OS predictive performance is the key criterion.

Business Forecasting