Tag Archives: macroeconomic forecasts

asset bubbles, forecasting asset bubbles, forecasting research, macroeconomic forecasting

The Worst Bear Market in History – Guest Post

March 14, 2014 Clive Jones

This is a fascinating case study of financial aberration, authored by Bryan Taylor, Ph.D., Chief Economist, Global Financial Data.

**********************************************************

Which country has the dubious distinction of suffering the worst bear market in history?

To answer this question, we ignore countries where the government closed down the stock exchange, leaving investors with nothing, as occurred in Russia in 1917 or Eastern European countries after World War II. We focus on stock markets that continued to operate during their equity-destroying disaster.

There is a lot of competition in this category. Almost every major country has had a bear market in which share prices have dropped over 80%, and some countries have had drops of over 90%. The Dow Jones Industrial Average dropped 89% between 1929 and 1932, the Greek Stock market fell 92.5% between 1999 and 2012, and adjusted for inflation, Germany’s stock market fell over 97% between 1918 and 1922.

The only consolation to investors is that the maximum loss on their investment is 100%, and one country almost achieved that dubious distinction. Cyprus holds the record for the worst bear market of all time in which investors have lost over 99% of their investment! Remember, this loss isn’t for one stock, but for all the shares listed on the stock exchange.

The Cyprus Stock Exchange All Share Index hit a high of 11443 on November 29, 1999, fell to 938 by October 25, 2004, a 91.8% drop. The index then rallied back to 5518 by October 31, 2007 before dropping to 691 on March 6, 2009. Another rally ensued to October 20, 2009 when the index hit 2100, but collapsed from there to 91 on October 24, 2013. The chart below makes any roller-coaster ride look boring by comparison (click to enlarge).

The fall from 11443 to 91 means that someone who invested at the top in 1999 would have lost 99.2% of their investment by 2013. And remember, this is for ALL the shares listed on the Cyprus Stock Exchange. By definition, some companies underperform the average and have done even worse, losing their shareholders everything.

For the people in Cyprus, this achievement only adds insult to injury. One year ago, in March 2013, Cyprus became the fifth Euro country to have its financial system rescued by a bail-out. At its height, the banking system’s assets were nine times the island’s GDP. As was the case in Iceland, that situation was unsustainable.

Since Germany and other paymasters for Ireland, Portugal, Spain and Greece were tired of pouring money down the bail-out drain, they demanded not only the usual austerity and reforms to put the country on the right track, but they also imposed demands on the depositors of the banks that had created the crisis, creating a “bail-in”.

As a result of the bail-in, debt holders and uninsured depositors had to absorb bank losses. Although some deposits were converted into equity, given the decline in the stock market, this provided little consolation. Banks were closed for two weeks and capital controls were imposed upon Cyprus. Not only did depositors who had money in banks beyond the insured limit lose money, but depositors who had money in banks were restricted from withdrawing their funds. The impact on the economy has been devastating. GDP has declined by 12%, and unemployment has gone from 4% to 17%.

On the positive side, when Cyprus finally does bounce back, large profits could be made by investors and speculators. The Cyprus SE All-Share Index is up 50% so far in 2014, and could move up further. Of course, there is no guarantee that the October 2013 will be the final low in the island’s fourteen-year bear market. To coin a phrase, Cyprus is a nice place to visit, but you wouldn’t want to invest there.

geopolitical risk, global business forecasts

Geopolitical Outlook 2014

March 11, 2014 Clive Jones

One service forecasting “staff” can provide executives and managers is a sort of list of global geopolitical risks. This is compelling only at certain times – and 2014 and maybe 2015 seem to be shaping up as one of these periods.

Just a theory, but, in my opinion, the sustained lackluster economic performance in the global economy, especially in Europe and also, by historic standards, the United States adds fuel to the fire of many conflicts. Conflict intensifies as people fight over an economic pie that is shrinking, or at least, not getting appreciably bigger, despite population growth and the arrival of new generations of young people on the scene.

Some Hotspots

Asia

First, the recent election in Thailand solved nothing, so far. The tally of results looks like it is going to take months – sustaining a kind of political vacuum after many violent protests. Economic growth is impacted, and the situation looks to be fluid.

But the big issue is whether China is going to experience significantly slower economic growth in 2014-2015, and perhaps some type of debt crisis.

For the first time, we are seeing municipal bond defaults and the run-on effects are not pretty.

The default on a bond payment by China’s Chaori Solar last week signalled a reassessment of credit risk in a market where even high-yielding debt had been seen as carrying an implicit state guarantee. On Tuesday, another solar company announced a second year of net losses, leading to a suspension of its stock and bonds on the Shanghai stock exchange and stoking fears that it, too, may default.

There are internal and external forces at work in the Chinese situation. It’s important to remember lackluster growth in Europe, one of China’s biggest customers, is bound to exert continuing downward pressure on Chinese economic growth.

Michael Pettis addresses some of these issues in his recent post Will emerging markets come back? Concluding that –

Emerging markets may well rebound strongly in the coming months, but any rebound will face the same ugly arithmetic. Ordinary households in too many countries have seen their share of total GDP plunge. Until it rebounds, the global imbalances will only remain in place, and without a global New Deal, the only alternative to weak demand will be soaring debt. Add to this continued political uncertainty, not just in the developing world but also in peripheral Europe, and it is clear that we should expect developing country woes only to get worse over the next two to three years.

Indonesia is experiencing persisting issues with the stability of its currency.

Europe

In general, economic growth in Europe is very slow, tapering to static and negative growth in key economies and the geographic periphery.

The European Commission, the executive arm of the European Union, on Tuesday forecast growth in the 28-county EU at 1.5 per cent this year and 2 per cent in 2015. But growth in the 18 euro zone countries, many of which are weighed down by high debt and lingering austerity, is forecast at only 1.2 per cent this year, up marginally from 1.1 per cent in the previous forecast, and 1.8 per cent next year.

France avoided recession by posting 0.3 % GDP in the final quarter of calendar year 2013.

Since margin of error for real GDP forecasts is on the order of +/- 2 percent, current forecasts are, in many cases, indistinguishable from a prediction of another recession.

And what could cause such a wobble?

Well, possibly increases in natural gas prices, as a result of political conflict between Russia and the west, or perhaps the outbreak of civil war in various eastern European locales?

The Ukraine

The issue of the Ukraine is intensely ideological and politicized and hard to evaluate without devolving into propaganda.

The population of the Ukraine has been in radical decline. Between 1991 and 2011 the Ukrainian population decreased by 11.8%, from 51.6 million to 45.5 million, apparently the result of very low fertility rates and high death rates. Transparency International also rates the Ukraine 144^th out of 177^th in terms of corruption – with 177^th being worst.

“Market reforms” such as would come with an International Monetary Fund (IMF) loan package would probably cause further hardship in the industrialized eastern areas of the country.

Stratfor and other emphasize the role of certain “oligarchs” in the Ukraine, operating more or less behind the scenes. I take it these immensely rich individuals in many cases were the beneficiaries of privatization of former state enterprise assets.

The Middle East

Again, politics is supreme. Political alliances between Saudi Arabia and others seeking to overturn Assad in Syria create special conditions, for sure. The successive governments in Egypt, apparently returning to rule by a strongman, are one layer – another layer is the increasingly challenged economic condition in the country – where fuel subsidies are commonly doled out to many citizens. Israel, of course, is a focus of action and reaction, and under Netanyahu is more than ready to rattle the sword. After Iraq and Afghanistan, it seems always possible for conflict to break out in unexpected directions in this region of the world.

A situation seems to be evolving in Turkey, which I do not understand, but may be involved with corruption scandals and spillovers from conflicts not only Syria but also the Crimea.

The United States

A good part of the US TV viewing audience has watched part or all of House of Cards, the dark, intricate story of corruption and intrigue at the highest levels of the US Congress. This show reinforces the view, already widely prevalent, that US politicians are just interested in fund-raising and feathering their own nest, and that they operate more or less in callous disregard or clear antagonism to the welfare of the people at large.

This is really too bad, in a way, since more than ever the US needs people to participate in the political process.

I wonder whether the consequence of this general loss of faith in the powers that be might fall naturally into the laps of more libertarian forces in US politics. State control and policies are so odious – how about trimming back the size of the central government significantly, including its ability to engage in foreign military and espionage escapades? Shades of Ron Paul and maybe his son, Senator Rand Paul of Kentucky.

South and Central America

Brazil snagged the Summer 2016 Olympics and is rushing to construct an ambitious number of venues around that vast country.

While the United States was absorbed in wars in the Middle East, an indigenous, socialist movement emerged in South American – centered around Venezuela and perhaps Bolivia, or Chile and Argentina. At least in Venezuela, sustaining these left governments after the charismatic leader passes from the scene is proving difficult.

Africa

Observing the ground rule that this sort of inventory has to be fairly easy, in order to be convincing – it seems that conflict is the order of the day across Africa. At the same time, the continent is moving forward, experiencing economic development, dealing with AIDS. Perhaps the currency situation in South Africa is the biggest geopolitical risk.

Bottom Line

The most optimistic take is that the outlook and risks now define a sort of interim period, perhaps lasting several years, when the level of conflict will increase at various hotspots. The endpoint, hopefully, will be the emergence of new technologies and products, new industries, which will absorb everyone in more constructive growth – perhaps growth defined ecologically, rather than merely in counting objects.

accuracy of forecasts, Big Data, data reduction, data science, financial forecasting, financial forecasts, macroeconomic forecasting, many predictors, partial least squares, predictive analytics, three pass regression filter (3PRF)

Three Pass Regression Filter – New Data Reduction Method

March 10, 2014 Clive Jones

Malcolm Gladwell’s 10,000 hour rule (for cognitive mastery) is sort of an inspiration for me. I picked forecasting as my field for “cognitive mastery,” as dubious as that might be. When I am directly engaged in an assignment, at some point or other, I feel the need for immersion in the data and in estimations of all types. This blog, on the other hand, represents an effort to survey and, to some extent, get control of new “tools” – at least in a first pass. Then, when I have problems at hand, I can try some of these new techniques.

Ok, so these remarks preface what you might call the humility of my approach to new methods currently being innovated. I am not putting myself on a level with the innovators, for example. At the same time, it’s important to retain perspective and not drop a critical stance.

The Working Paper and Article in the Journal of Finance

Probably one of the most widely-cited recent working papers is Kelly and Pruitt’s three pass regression filter (3PRF). The authors, shown above, are with the University of Chicago, Booth School of Business and the Federal Reserve Board of Governors, respectively, and judging from the extensive revisions to the 2011 version, they had a bit of trouble getting this one out of the skunk works.

Recently, however, Kelly and Pruit published an important article in the prestigious Journal of Finance called Market Expectations in the Cross-Section of Present Values. This article applies a version of the three pass regression filter to show that returns and cash flow growth for the aggregate U.S. stock market are highly and robustly predictable.

I learned of a published application of the 3PRF from Francis X. Dieblod’s blog, No Hesitations, where Diebold – one of the most published authorities on forecasting – writes

Recent interesting work, moreover, extends PLS in powerful ways, as with the Kelly-Pruitt three-pass regression filter and its amazing apparent success in predicting aggregate equity returns.

What is the 3PRF?

The working paper from the Booth School of Business cited at a couple of points above describes what might be cast as a generalization of partial least squares (PLS). Certainly, the focus in the 3PRF and PLS is on using latent variables to predict some target.

I’m not sure, though, whether 3PRF is, in fact, more of a heuristic, rather than an algorithm.

What I mean is that the three pass regression filter involves a procedure, described below.

(click to enlarge).

Here’s the basic idea –

Suppose you have a large number of potential regressors x_i ε X, i=1,..,N. In fact, it may be impossible to calculate an OLS regression, since N > T the number of observations or time periods.

Furthermore, you have proxies z_j ε Z, I = 1,..,L – where L is significantly less than the number of observations T. These proxies could be the first several principal components of the data matrix, or underlying drivers which theory proposes for the situation. The authors even suggest an automatic procedure for generating proxies in the paper.

And, finally, there is the target variable y_t which is a column vector with T observations.

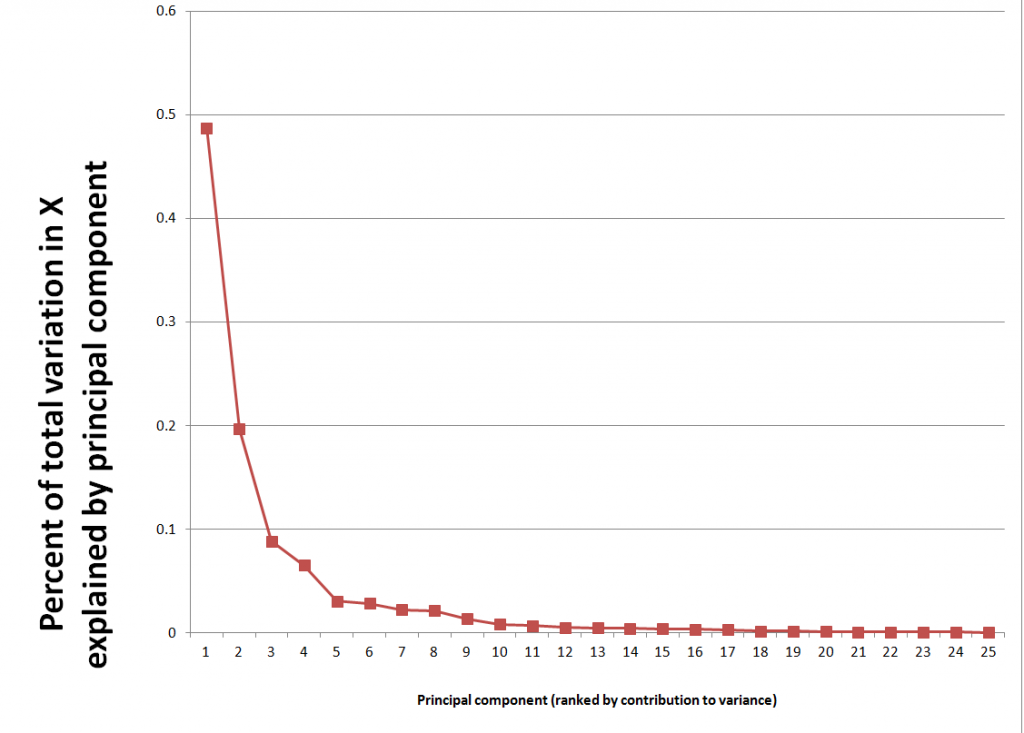
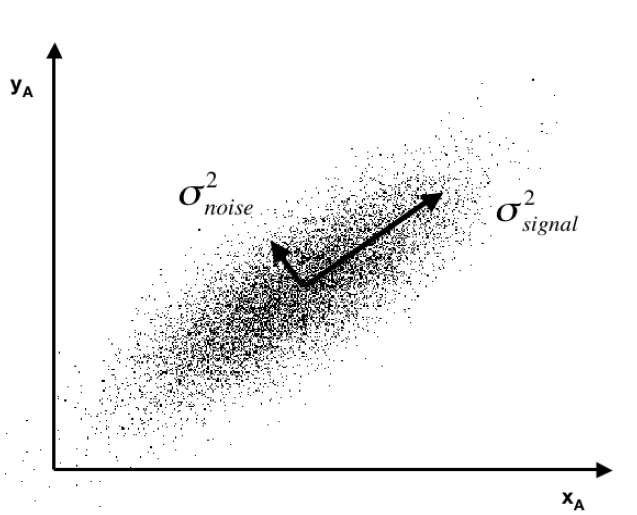
Latent factors in a matrix F drive both the proxies in Z and the predictors in X. Based on macroeconomic research into dynamic factors, there might be only a few of these latent factors – just as typically only a few principal components account for the bulk of variation in a data matrix.

Now here is a key point – as Kelly and Pruitt present the 3PRF, it is a leading indicator approach when applied to forecasting macroeconomic variables such as GDP, inflation, or the like. Thus, the time index for y_t ranges from 2,3,…T+1, while the time indices of all X and Z variables and the factors range from 1,2,..T. This means really that all the x and z variables are potentially leading indicators, since they map conditions from an earlier time onto values of a target variable at a subsequent time.

What Table 1 above tells us to do is –

Run an ordinary least square (OLS) regression of the x_i in X onto the z_j in X, where T ranges from 1 to T and there are N variables in X and L << T variables in Z. So, in the example discussed below, we concoct a spreadsheet example with 3 variables in Z, or three proxies, and 10 predictor variables x_i in X (I could have used 50, but I wanted to see whether the method worked with lower dimensionality). The example assumes 40 periods, so t = 1,…,40. There will be 40 different sets of coefficients of the z_j as a result of estimating these regressions with 40 matched constant terms.
OK, then we take this stack of estimates of coefficients of the z_j and their associated constants and map them onto the cross sectional slices of X for t = 1,..,T. This means that, at each period t, the values of the cross-section. x_i,t, are taken as the dependent variable, and the independent variables are the 40 sets of coefficients (plus constant) estimated in the previous step for period t become the predictors.
Finally, we extract the estimate of the factor loadings which results, and use these in a regression with target variable as the dependent variable.

This is tricky, and I have questions about the symbolism in Kelly and Pruitt’s papers, but the procedure they describe does work. There is some Matlab code here alongside the reference to this paper in Professor Kelly’s research.

At the same time, all this can be short-circuited (if you have adequate data without a lot of missing values, apparently) by a single humungous formula –

Here, the source is the 2012 paper.

Spreadsheet Implementation

Spreadsheets help me understand the structure of the underlying data and the order of calculation, even if, for the most part, I work with toy examples.

So recently, I’ve been working through the 3PRF with a small spreadsheet.

Generating the factors:I generated the factors as two columns of random variables (=rand()) in Excel. I gave the factors different magnitudes by multiplying by different constants.

Generating the proxies Z and predictors X. Kelly and Pruitt call for the predictors to be variance standardized, so I generated 40 observations on ten sets of x_iby selecting ten different coefficients to multiply into the two factors, and in each case I added a normal error term with mean zero and standard deviation 1. In Excel, this is the formula =norminv(rand(),0,1).

Basically, I did the same drill for the three z_j — I created 40 observations for z1, z2, and z3 by multiplying three different sets of coefficients into the two factors and added a normal error term with zero mean and variance equal to 1.

Then, finally, I created y_t by multiplying randomly selected coefficients times the factors.

After generating the data, the first pass regression is easy. You just develop a regression with each predictor x_i as the dependent variable and the three proxies as the independent variables, case-by-case, across the time series for each. This gives you a bunch of regression coefficients which, in turn, become the explanatory variables in the cross-sectional regressions of the second step.

The regression coefficients I calculated for the three proxies, including a constant term, were as follows – where the 1^st row indicates the regression for x₁ and so forth.

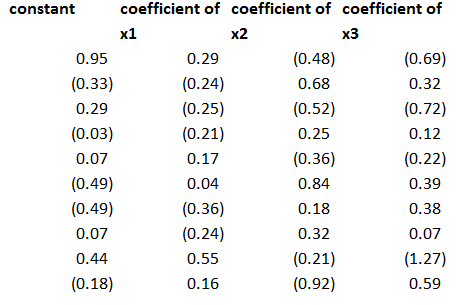
This second step is a little tricky, but you just take all the values of the predictor variables for a particular period and designate these as the dependent variables, with the constant and coefficients estimated in the previous step as the independent variables. Note, the number of predictors pairs up exactly with the number of rows in the above coefficient matrix.

This then gives you the factor loadings for the third step, where you can actually predict y_t (really y_t+1 in the 3PRF setup). The only wrinkle is you don’t use the constant terms estimated in the second step, on the grounds that these reflect “idiosyncratic” effects, according to the 2011 revision of the paper.

Note the authors describe this as a time series approach, but do not indicate how to get around some of the classic pitfalls of regression in a time series context. Obviously, first differencing might be necessary for nonstationary time series like GDP, and other data massaging might be in order.

Bottom line – this worked well in my first implementation.

To forecast, I just used the last regression for y_t+1 and then added ten more cases, calculating new values for the target variable with the new values of the factors. I used the new values of the predictors to update the second step estimate of factor loadings, and applied the last third pass regression to these values.

Here are the forecast errors for these ten out-of-sample cases.

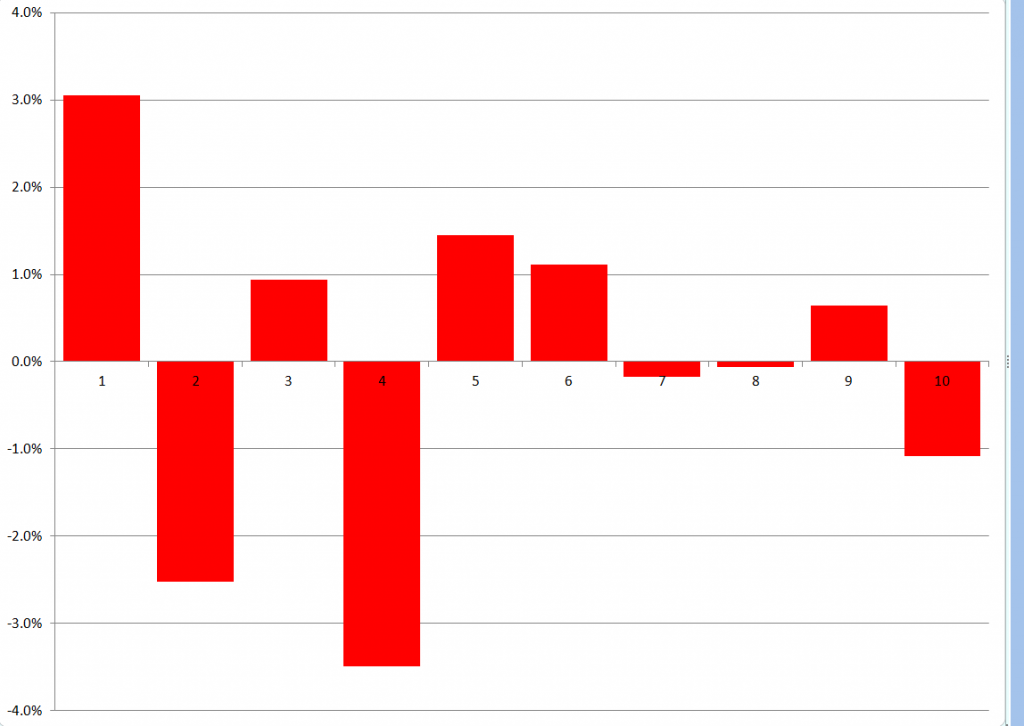
Not bad for a first implementation.

Why Is Three Pass Regression Important?

3PRF is a fairly “clean” solution to an important problem, relating to the issue of “many predictors” in macroeconomics and other business research.

Noting that if the predictors number near or more than the number of observations, the standard ordinary least squares (OLS) forecaster is known to be poorly behaved or nonexistent, the authors write,

How, then, does one effectively use vast predictive information? A solution well known in the economics literature views the data as generated from a model in which latent factors drive the systematic variation of both the forecast target, y, and the matrix of predictors, X. In this setting, the best prediction of y is infeasible since the factors are unobserved. As a result, a factor estimation step is required. The literature’s benchmark method extracts factors that are significant drivers of variation in X and then uses these to forecast y. Our procedure springs from the idea that the factors that are relevant to y may be a strict subset of all the factors driving X. Our method, called the three-pass regression filter (3PRF), selectively identifies only the subset of factors that influence the forecast target while discarding factors that are irrelevant for the target but that may be pervasive among predictors. The 3PRF has the advantage of being expressed in closed form and virtually instantaneous to compute.

So, there are several advantages, such as (1) the solution can be expressed in closed form (in fact as one complicated but easily computable matrix expression), and (2) there is no need to employ maximum likelihood estimation.

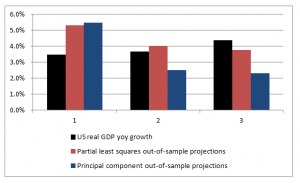
Furthermore, 3PRF may outperform other approaches, such as principal components regression or partial least squares.

The paper illustrates the forecasting performance of 3PRF with real-world examples (as well as simulations). The first relates to forecasts of macroeconomic variables using data such as from the Mark Watson database mentioned previously in this blog. The second application relates to predicting asset prices, based on a factor model that ties individual assets’ price-dividend ratios to aggregate stock market fluctuations in order to uncover investors’ discount rates and dividend growth expectations.

accuracy of forecasts, Big Data, data science, downloadable texts on statistics and forecasting, macroeconomic forecasting, many predictors, partial least squares, predictive analytics, principal component models and forecasts

Partial Least Squares and Principal Components

March 9, 2014 Clive Jones

I’ve run across outstanding summaries of “partial least squares” (PLS) research recently – for example Rosipal and Kramer’s Overview and Recent Advances in Partial Least Squares and the 2010 Handbook of Partial Least Squares.

Partial least squares (PLS) evolved somewhat independently from related statistical techniques, owing to what you might call family connections. The technique was first developed by Swedish statistician Herman Wold and his son, Svante Wold, who applied the method in particular to chemometrics. Rosipal and Kramer suggest that the success of PLS in chemometrics resulted in a lot of applications in other scientific areas including bioinformatics, food research, medicine, [and] pharmacology..

Someday, I want to look into “path modeling” with PLS, but for now, let’s focus on the comparison between PLS regression and principal component (PC) regression. This post develops a comparison with Matlab code and macroeconomics data from Mark Watson’s website at Princeton.

The Basic Idea Behind PC and PLS Regression

Principal component and partial least squares regression share a couple of features.

Both, for example, offer an approach or solution to the problem of “many predictors” and multicollinearity. Also, with both methods, computation is not transparent, in contrast to ordinary least squares (OLS). Both PC and PLS regression are based on iterative or looping algorithms to extract either the principal components or underlying PLS factors and factor loadings.

PC Regression

The first step in PC regression is to calculate the principal components of the data matrix X. This is a set of orthogonal (which is to say completely uncorrelated) vectors which are weighted sums of the predictor variables in X.

This is an iterative process involving transformation of the variance-covariance or correlation matrix to extract the eigenvalues and eigenvectors.

Then, the data matrix X is multiplied by the eigenvectors to obtain the new basis for the data – an orthogonal basis. Typically, the first few (the largest) eigenvalues – which explain the largest proportion of variance in X – and their associated eigenvectors are used to produce one or more principal components which are regressed onto Y. This involves a dimensionality reduction, as well as elimination of potential problems of multicollinearity.

PLS Regression

The basic idea behind PLS regression, on the other hand, is to identify latent factors which explain the variation in both Y and X, then use these factors, which typically are substantially fewer in number than k, to predict Y values.

Clearly, just as in PC regression, the acid test of the model is how it performs on out-of-sample data.

The reason why PLS regression often outperforms PC regression, thus, is that factors which explain the most variation in the data matrix may not, at the same time, explain the most variation in Y. It’s as simple as that.

Matlab example

I grabbed some data from Mark Watson’s website at Princeton — from the links to a recent paper called Generalized Shrinkage Methods for Forecasting Using Many Predictors (with James H. Stock), Journal of Business and Economic Statistics, 30:4 (2012), 481-493.Download Paper (.pdf). Download Supplement (.pdf), Download Data and Replication Files (.zip). The data include the following variables, all expressed as year-over-year (yoy) growth rates: The first variable – real GDP – is taken as the forecasting target. The time periods of all other variables are lagged one period (1 quarter) behind the quarterly values of this target variable.

Matlab makes calculation of both principal component and partial least squares regressions easy.

The command to extract principal components is

[coeff, score, latent]=princomp(X)

Here X the data matrix, and the entities in the square brackets are vectors or matrices produced by the algorithm. It’s possible to compute a principal components regression with the contents of the matrix score. Generally, the first several principal components are selected for the regression, based on the importance of a component or its associated eigenvalue in latent. The following scree chart illustrates the contribution of the first few principal components to explaining the variance in X.

The relevant command for regression in Matlab is

b=regress(Y,score(:,1:6))

where b is the column vector of estimated coefficients and the first six principal components are used in place of the X predictor variables.

The Matlab command for a partial least square regresssion is

[XL,YL,XS,YS,beta] = plsregress(X,Y,ncomp)

where ncomp is the number of latent variables of components to be utilized in the regression. There are issues of interpreting the matrices and vectors in the square brackets, but I used this code –

data=xlsread(‘stock.xls’); X=data(1:47,2:79); y = data(2:48,1);

[XL,yl,XS,YS,beta] = plsregress(X,y,10); yfit = [ones(size(X,1),1) X]*beta;

lookPLS=[y yfit]; ZZ=data(48:50,2:79);newy=data(49:51,1);

new=[ones(3,1) ZZ]*beta; out=[newy new];

The bottom line is to test the estimates of the response coefficients on out-of-sample data.

The following chart shows that PLS outperforms PC, although the predictions of both are not spectacularly accurate.

Commentary

There are nuances to what I have done which help explain the dominance of PLS in this situation, as well as the weakly predictive capabilities of both approaches.

First, the target variable is quarterly year-over-year growth of real US GDP. The predictor set X contains 78 other macroeconomic variables, all expressed in terms of yoy (year-over-year) percent changes.

Again, note that the time period of all the variables or observations in X are lagged one quarter from the values in Y, or the values or yoy quarterly percent growth of real US GDP.

This means that we are looking for a real, live leading indicator. Furthermore, there are plausibly common factors in the Y series shared with at least some of the X variables. For example, the percent changes of a block of variables contained in real GDP are included in X, and by inspection move very similarly with the target variable.

Other Example Applications

There are at least a couple of interesting applied papers in the Handbook of Partial Least Squares – a downloadable book in the Springer Handbooks of Computational Statistics. See –

Chapter 20 A PLS Model to Study Brand Preference: An Application to the Mobile Phone Market

Chapter 22 Modeling the Impact of Corporate Reputation on Customer Satisfaction and Loyalty Using Partial Least Squares

Another macroeconomics application from the New York Fed –

“Revisiting Useful Approaches to Data-Rich Macroeconomic Forecasting”

http://www.newyorkfed.org/research/staff_reports/sr327.pdf

Finally, the software company XLStat has a nice, short video on partial least squares regression applied to a marketing example.

ARIMA models, Big Data, macroeconomic forecasting, principal component models and forecasts

Forecasting and Data Analysis – Principal Component Regression

February 26, 2014 Clive Jones

I get excited that principal components offer one solution to the problem of the curse of dimensionality – having fewer observations on the target variable to be predicted, than there are potential drivers or explanatory variables.

It seems we may have to revise the idea that simpler models typically outperform more complex models.

Principal component (PC) regression has seen a renaissance since 2000, in part because of the work of James Stock and Mark Watson (see also) and Bai in macroeconomic forecasting (and also because of applications in image processing and text recognition).

Let me offer some PC basics and explore an example of PC regression and forecasting in the context of macroeconomics with a famous database.

Dynamic Factor Models in Macroeconomics

Stock and Watson have a white paper, updated several times, in PDF format at this link

stock watson generalized shrinkage June _2012.pdf

They write in the June 2012 update,

We find that, for most macroeconomic time series, among linear estimators the DFM forecasts make efficient use of the information in the many predictors by using only a small number of estimated factors. These series include measures of real economic activity and some other central macroeconomic series, including some interest rates and monetary variables. For these series, the shrinkage methods with estimated parameters fail to provide mean squared error improvements over the DFM. For a small number of series, the shrinkage forecasts improve upon DFM forecasts, at least at some horizons and by some measures, and for these few series, the DFM might not be an adequate approximation. Finally, none of the methods considered here help much for series that are notoriously difficult to forecast, such as exchange rates, stock prices, or price inflation.

Here DFM refers to dynamic factor models, essentially principal components models which utilize PC’s for lagged data.

What’s a Principal Component?

Essentially, you can take any bundle of data and compute the principal components. If you mean-center and (in most cases) standardize the data, the principal components divide up the variance of this data, based on the size of their associated eigenvalues. The associated eigenvectors can be used to transform the data into an equivalent and same size set of orthogonal vectors. Really, the principal components operate to change the basis of the data, transforming it into an equivalent representation, but one in which all the variables have zero correlation with each other.

The Wikipaedia article on principal components is useful, but there is no getting around the fact that principal components can only really be understood with matrix algebra.

Often you see a diagram, such as the one below, showing a cloud of points distributed around a line passing through the origin of a coordinate system, but at an acute angle to those coordinates.

This illustrates dimensionality reduction with principal components. If we express all these points in terms of this rotated set of coordinates, one of these coordinates – the signal – captures most of the variation in the data. Projections of the datapoints onto the second principal component, therefore, account for much less variance.

Principal component regression characteristically specifies only the first few principal components in the regression equation, knowing that, typically, these explain the largest portion of the variance in the data.

It’s also noteworthy that some researchers are talking about “targeted” principal components. So the first few principal components account for the largest, the next largest, and so on amount of variance in the data. However, the “data” in this context does not include the information we have on the target variable. Targeted principal components therefore involves first developing the simple correlations between the target variable and all the potential predictors, then ordering these potential predictors from highest to lowest correlation. Then, by one means or another, you establish a cutoff, below which you exclude weak potential predictors from the data matrix you use to compute the principal components. Interesting approach which makes sense. Testing it with a variety of examples seems in order.

PC Regression and Forecasting – A Macroeconomics Example

I downloaded a trial copy of XLSTAT – an Excel add-in with a well-developed set of principal component procedures. In the past, I’ve used SPSS and SAS on corporate networked systems. Now I am using Matlab and GAUSS for this purpose.

The problem is what does it mean to have a time series of principal components? Over the years, there have been relevant discussions – Jolliffe’s key work, for example, and more recent papers.

The problem with time series, apart from the temporal interdependencies, is that you always are calculating the PC’s over different data, as more data comes in. What does this do to the PC’s or factor scores? Do they evolve gradually? Can you utilize the factor scores from a smaller dataset to predict subsequent values of factor scores estimated over an augmented dataset?

Based on a large macroeconomic dataset I downloaded from Mark Watson’s page, I think the answer can be a qualified “yes” to several of these questions. The Mark Watson dataset contains monthly observations on 106 macroeconomic variables for the period 1950 to 2006.

For the variables not bounded within a band, I calculated year-over-year (yoy) growth rates for each monthly observation. Then, I took first differences again over 12 months. These transformations eliminated trends, which mess up the PC computations (basically, if you calculate PC’s with a set of increasing variables, the first PC will represent a common growth factor, and is almost useless for modeling purposes.) The result of my calculations was to center each series at nearly zero, and to make the variability of each series comparable – so I did not standardize.

Anyway, using XLSTAT and Forecast Pro – I find that the factor scores

(a) Evolve slowly as you add more data.

(b) Factor scores for smaller datasets provide insight into subsequent factor scores one to several months ahead.

(c) Amazingly, turning points of the first principal component, which I have studied fairly intensively, are remarkably predictable.

So what are we looking at here (click to enlarge)?

Well, the top chart is the factor score for the first PC, estimated over data to May 1975, with a forecast indicated by the red line at the right of the graph. This forecast produces values which are very close to the factor score values for data estimated to May 1976 – where both datasets begin in 1960. Not only that, but we have here an example of prediction of a turning point bigtime.

Of course this is the magic of Box-Jenkins, since, this factor score series is best estimated, according to Forecast Pro, with an ARIMA model.

I’m encouraged by this exercise to think that it may be possible to go beyond the lagged variable specification in many of these DFM’s to a contemporaneous specification, where the target variable forecasts are based on extrapolations of the relevant PC’s.

In any case, for applied business modeling, if we got something like a medical device new order series (suitably processed data) linked with these macro factor scores, it could be interesting – and we might get something that is not accessible with ordinary methods of exponential smoothing.

Underlying Theory of PC’s

Finally, I don’t think it is possible to do much better than to watch Andrew Ng at Stanford in Lectures 14 and 15. I recommend skipping to 17:09 – seventeen minutes and nine seconds – into Lecture 14, where Ng begins the exposition of principal components. He winds up this Lecture with a fascinating illustration of high dimensionality principal component analysis applied to recognizing or categorizing faces in photographs at the end of this lecture. Lecture 15 also is very useful – especially as it highlights the role of the Singular Value Decomposition (SVD) in actually calculating principal components.

Lecture 14

http://www.youtube.com/watch?v=ey2PE5xi9-A

Lecture 15

http://www.youtube.com/watch?v=QGd06MTRMHs

accuracy of forecasts, forecasting research, macroeconomic forecasting

The Accuracy of Macroeconomics Forecasts – Survey of Professional Forecasters

February 25, 2014 Clive Jones

The Philadelphia Federal Reserve Bank maintains historic records of macroeconomic forecasts from the Survey of Professional Forecasters (SPF). These provide an outstanding opportunity to assess forecasting accuracy in macroeconomics.

For example, in 2014, what is the chance the “steady as she goes” forecast from the current SPF is going to miss a downturn 1, 2, or 3 quarters into the future?

1-Quarter-Ahead Forecast Performance on Real GDP

Here is a chart I’ve ginned up for a 1-quarter ahead performance of the SPF forecasts of real GDP since 1990.

The blue line is the forecast growth rate for real GDP from the SPF on a 1-quarter-ahead basis. The red line is the Bureau of Economic Analysis (BEA) final number for the growth rate for the relevant quarters. The growth rates in both instances are calculated on a quarter-over-quarter basis and annualized.

Side-stepping issues regarding BEA revisions, I used BEA final numbers for the level and growth of real GDP by quarter. This may not completely fair to the SPF forecasters, but it is the yardstick SPF is usually judged by its “consumers.”

Forecast errors for the 1-quarter-ahead forecasts, calculated on this basis, average about 2 percent in absolute value.

They also exhibit significant first order autocorrelation, as is readily suggested by the chart above. So, the SPF tends to under-predict during expansion phases of the business cycle and over-predict during contraction phases.

Currently, the SPF 2014:Q1 forecast for 2014:Q2 is for 3.0 percent real growth of GDP, so maybe it’s unlikely that an average error for this forecast would result in actual 2014:Q2 growth dipping into negative territory.

2-Quarter-Ahead Forecast Performance on Real GDP

Errors for the 2-quarter-ahead SPF forecast, judged against BEA final numbers for real GDP growth, only rise to about 2.14 percent.

However, I am interested in more than the typical forecast error associated with forecasts of real Gross Domestic Product (GDP) on a 1-, 2-, or 3- quarter ahead forecast horizon.

Rather, I’m curious whether the SPF is likely to catch a
downturn over these forecast horizons, given that one will occur.

So if we just look at recessions in this period, in 2001, 2002-2003, and 2008-2009, the performance significantly deteriorates. This can readily be seen in the graph for 1-quarter-ahead forecast errors shown above in 2008 when the consensus SPF forecast indicated a slight recovery for real GDP in exactly the quarter it totally tanked.

Bottom Line

In general, the SPF records provide vivid documentation of the difficulty of predicting turning points in key macroeconomic time series, such as GDP, consumer spending, investment, and so forth. At the same time, the real-time macroeconomic databases provided alongside the SPF records offer interesting opportunities for second- and third-guessing both the experts and the agencies responsible for charting US macroeconomics.

Additional Background

The Survey of Professional Forecasters is the oldest quarterly survey of macroeconomic forecasts in the United States. It dates back to 1968, when it was conducted by the American Statistical Association and the National Bureau of Economic Research (NBER). In 1990, the Federal Reserve Bank of Philadelphia assumed responsibility, and, today, devotes a special section on its website to the SPF, as well “Historical SPF Forecast Data.”

Current and recent contributors to the SPF include “celebrity forecasters” highlighted in other posts here, as well as bank-associated and university-affiliated forecasters.

The survey’s timing is geared to the release of the Bureau of Economic Analysis’ advance report of the national income and product accounts. This report is released at the end of the first month of each quarter. It contains the first estimate of GDP (and components) for the previous quarter. Survey questionnaires are sent after this report is released to the public. The survey’s questionnaires report recent historical values of the data from the BEA’s advance report and the most recent reports of other government statistical agencies. Thus, in submitting their projections, panelists’ information includes data reported in the advance report.

Recent participants include:

Lewis Alexander, Nomura Securities; Scott Anderson, Bank of the West (BNP Paribas Group); Robert J. Barbera, Johns Hopkins University Center for Financial Economics; Peter Bernstein, RCF Economic and Financial Consulting, Inc.; Christine Chmura, Ph.D. and Xiaobing Shuai, Ph.D., Chmura Economics & Analytics; Gary Ciminero, CFA, GLC Financial Economics; Julia Coronado, BNP Paribas; David Crowe, National Association of Home Builders; Nathaniel Curtis, Navigant; Rajeev Dhawan, Georgia State University; Shawn Dubravac, Consumer Electronics Association; Gregory Daco, Oxford Economics USA, Inc.; Michael R. Englund, Action Economics, LLC; Timothy Gill, NEMA; Matthew Hall and Daniil Manaenkov, RSQE, University of Michigan; James Glassman, JPMorgan Chase & Co.; Jan Hatzius, Goldman Sachs; Peter Hooper, Deutsche Bank Securities, Inc.; IHS Global Insight; Fred Joutz, Benchmark Forecasts and Research Program on Forecasting, George Washington University; Sam Kahan, Kahan Consulting Ltd. (ACT Research LLC); N. Karp, BBVA Compass; Walter Kemmsies, Moffatt & Nichol; Jack Kleinhenz, Kleinhenz & Associates, Inc.; Thomas Lam, OSK-DMG/RHB; L. Douglas Lee, Economics from Washington; Allan R. Leslie, Economic Consultant; John Lonski, Moody’s Capital Markets Group; Macroeconomic Advisers, LLC; Dean Maki, Barclays Capital; Jim Meil and Arun Raha, Eaton Corporation; Anthony Metz, Pareto Optimal Economics; Michael Moran, Daiwa Capital Markets America; Joel L. Naroff, Naroff Economic Advisors; Michael P. Niemira, International Council of Shopping Centers; Luca Noto, Anima Sgr; Brendon Ogmundson, BC Real Estate Association; Martin A. Regalia, U.S. Chamber of Commerce; Philip Rothman, East Carolina University; Chris Rupkey, Bank of Tokyo-Mitsubishi UFJ; John Silvia, Wells Fargo; Allen Sinai, Decision Economics, Inc.; Tara M. Sinclair, Research Program on Forecasting, George Washington University; Sean M. Snaith, Ph.D., University of Central Florida; Neal Soss, Credit Suisse; Stephen Stanley, Pierpont Securities; Charles Steindel, New Jersey Department of the Treasury; Susan M. Sterne, Economic Analysis Associates, Inc.; Thomas Kevin Swift, American Chemistry Council; Richard Yamarone, Bloomberg, LP; Mark Zandi, Moody’s Analytics.

forecast accuracy, forecast competitions, forecasting research, global business forecasts, macroeconomic forecasting

Sayings of the Top Macro Forecasters

February 8, 2014 Clive Jones

Yesterday, I posted the latest Bloomberg top twenty US macroeconomic forecaster rankings, also noting whether this current crop made it into the top twenty in previous “competitions” for November 2010-November 2012 or November 2009-November 2011.

It turns out the Bloomberg top twenty is relatively stable. Seven names or teams on the 2014 list appear in both previous competitions. Seventeen made it into the top twenty at least twice in the past three years.

But who are these people and how can we learn about their forecasts on a real-time basis?

Well, as you might guess, this is a pretty exclusive club. Many are Chief Economists and company Directors in investment advisory organizations serving private clients. Several did a stint on the staff of the Federal Reserve earlier in their career. Their public interface is chiefly through TV interviews, especially Bloomberg TV, or other media coverage.

I found a couple of exceptions, however – Michael Carey and Russell Price.

Michael Carey and Crédit Agricole

Michael Carey is Chief Economist North America Crédit Agricole CIB. He ranked 14, 7, and 5, based on his average scores for his forecasts of the key indicators in these three consecutive competitions. He apparently is especially good on employment forecasts.

Carey is a lead author for a quarterly publication from Crédit Agricole called Prospects Macro.

The Summary for the current issue (1^st Quarter 2014) caught my interest –

On the economic trend front, an imperfect normalisation seems to be getting underway. One may talk about a normalisation insofar as – unlike the two previous financial years – analysts have forecast a resumption of synchronous growth in the US, the Eurozone and China. US growth is forecast to rise from 1.8% in 2013 to 2.7%; Eurozone growth is slated to return to positive territory, improving from -0.4% to +1.0%; while Chinese growth is forecast to dip slightly, from 7.7% to 7.2%, which does not appear unwelcome nor requiring remedial measures. The imperfect character of the forecast normalisation quickly emerges when one looks at the growth predictions for 2015. In each of the three regions, growth is not gathering pace, or only very slightly. It is very difficult to defend the idea of a cyclical mechanism of self-sustaining economic acceleration. This observation seems to echo an ongoing academic debate: growth in industrialised countries seems destined to be weak in the years ahead. Partly, this is because structural growth drivers seem to be hampered (by demographics, debt and technology shocks), and partly because real interest rates seem too high and difficult to cut, with money-market rates that are already virtually at zero and low inflation, which is likely to last. For the markets, monetary policies can only be ‘reflationist’. Equities prices will rise until they come upagainst the overvaluation barrier and long-term rates will continue to climb, but without reaching levels justified by growth and inflation fundamentals.

I like that – an “imperfect normalization” (note the British spelling). A key sentence seems to be “It is very difficult to defend the idea of a cyclical mechanism of self-sustaining economic acceleration.”

So maybe the issue is 2015.

The discussion of emerging markets prospects is well-worth quoting also.

At 4.6% (and 4.2% excluding China), average growth in 2013 across all emerging countries seems likely to have been at its lowest since 2002, apart from the crisis year of 2009. Despite the forecast slowdown in China (7.2%, after 7.7%), the overall pace of growth for EMs is likely to pick up slightly in 2014 (to 4.8%, and 4.5% excluding China). The trend is likely to continue through 2015. This modest rebound, despite the poor growth figures expected from Brazil, is due to the slightly improved performance of a few other large emerging economies such as India, and above all Mexico, South Korea and some Central European countries. As regards the content of this growth, it is investment that should improve, on the strength of better growth prospects in the industrialised countries…

The growth differential with the industrialised countries has narrowed to around 3%, whereas it had stood at around 5% between 2003 and 2011…

This situation is unlikely to change radically in 2014. Emerging markets should continue to labour under two constraints. First off, the deterioration in current accounts has worsened as a result of fairly weak external demand, stagnating commodity prices, and domestic demand levels that are still sticky in many emerging countries…Commodity-exporting countries and most Asian exporters of manufactured goods are still generating surpluses, although these are shrinking. Conversely, large emerging countries such as India, Indonesia, Brazil, Turkey and South Africa are generating deficits that are in some cases reaching alarming proportions – especially in Turkey. These imbalances could restrict growth in 2014-15, either by encouraging governments to tighten monetary conditions or by limiting access to foreign financing.

Secondly, most emerging countries are now paying the price for their reluctance to embrace reform in the years of strong global growth prior to the great global financial crisis. This price is today reflected in falling potential growth levels in some emerging countries, whose weaknesses are now becoming increasingly clear. Examples are Russia and its addiction to commodities; Brazil and its lack of infrastructure, low savings rate and unruly inflation; India and its lack of infrastructure, weakening rate of investment and political dependence of the Federal state on the federated states. Unfortunately, the less favourable international situation (think rising interest rates) and local contexts (eg, elections in India and Brazil in 2014) make implementing significant reforms more difficult over the coming quarters. This is having a depressing effect on prospects for growth

I’m subscribing to notices of updates to this and other higher frequency reports from Crédit Agricole.

Russell Price and Ameriprise

Russell Price, younger than Michael Carey, was Number 7 on the current Bloomberg list of top US macro forecasters, ranking 16 the previous year. He has his own monthly publication with Ameriprise called Economic Perspectives.

The current issue dated January 28, 2014 is more US-centric, and projects a “modest pace of recovery” for the “next 3 to 5 years.” Still, the current issue warns that analyst projections of company profits are probably “overly optimistic.”

I need to read one or two more of the issues to properly evaluate, but Economic Perspectives is definitely a cut above the average riff on macroeconomic prospects.

Another Way To Tap Into Forecasts of the Top Bloomberg Forecasters

The Wall Street Journal’s Market Watch is another way to tap into forecasts from names and teams on the top Bloomberg lists.

The Market Watch site publishes weekly median forecasts based on the 15 economists who have scored the highest in our contest over the past 12 months, as well as the forecasts of the most recent winner of the Forecaster of the Month contest.

The economists in the Market Watch consensus forecast include many currently or recently in the top twenty Bloomberg list – Jim O’Sullivan of High Frequency Economics, Michael Feroli of J.P. Morgan, Paul Edelstein of IHS Global Insight, Brian Jones of Société Générale, Spencer Staples of EconAlpha, Ted Wieseman of Morgan Stanley, Jan Hatzius’s team at Goldman Sachs, Stephen Stanley of Pierpont Securities, Avery Shenfeld of CIBC, Maury Harris’s team at UBS, Brian Wesbury and Robert Stein of First Trust, Jeffrey Rosen of Briefing.com, Paul Ashworth of Capital Economics, Julia Coronado of BNP Paribas, and Eric Green’s team at TD Securities.

And I like the format of doing retrospectives on these consensus forecasts, in tables such as this:

So what’s the bottom line here? Well, to me, digging deeper into the backgrounds of these top ranked forecasters, finding access to their current thinking is all part of improving competence.

I can think of no better mantra than Malcolm Gladwell’s 10,000 Hour Rule –

bagging, downloadable texts on statistics and forecasting, forecasting turning points, macroeconomic forecasting, random walk

The On-Coming Tsunami of Data Analytics

January 3, 2014 Clive Jones

More than 25,000 visited businessforecastblog, March 2012-December 2013, some spending hours on the site. Interest ran nearly 200 visitors a day in December, before my ability to post was blocked by a software glitch, and we did this re-boot.

Now I have hundreds of posts offline, pertaining to several themes, discussed below. How to put this material back up – as reposts, re-organized posts, or as longer topic summaries?

There’s a silver lining. This forces me to think through forecasting, predictive and data analytics.

One thing this blog does is compile information on which forecasting and data analytics techniques work, and, to some extent, how they work, how key results are calculated. I’m big on computation and performance metrics, and I want to utilize the SkyDrive more extensively to provide full access to spreadsheets with worked examples.

Often my perspective is that of a “line worker” developing sales forecasts. But there is another important focus – business process improvement. The strength of a forecast is measured, ultimately, by its accuracy. Efforts to improve business processes, on the other hand, are clocked by whether improvement occurs – whether costs of reaching customers are lower, participation rates higher, customer retention better or in stabilization mode (lower churn), and whether the executive suite and managers gain understanding of who the customers are. And there is a third focus – that of the underlying economics, particularly the dynamics of the institutions involved, such as the US Federal Reserve.

Right off, however, let me say there is a direct solution to forecasting sales next quarter or in the coming budget cycle. This is automatic forecasting software, with Forecast Pro being one of the leading products. Here’s a YouTube video with the basics about that product.

You can download demo versions and participate in Webinars, and attend the periodic conferences organized by Business Forecast Systems showcasing user applications in a wide variety of companies.

So that’s a good solution for starters, and there are similar products, such as the SAS/ETS time series software, and Autobox.

So what more would you want?

Well, there’s need for background information, and there’s a lot of terminology. It’s useful to know about exponential smoothing and random walks, as well as autoregressive and moving averages. Really, some reaches of this subject are arcane, but nothing is worse than a forecast setup which gains the confidence of stakeholders, and then falls flat on its face. So, yes, eventually, you need to know about “pathologies” of the classic linear regression (CLR) model – heteroscedasticity, autocorrelation, multicollinearity, and specification error!

And it’s good to gain this familiarity in small doses, in connection with real-world applications or even forecasting personalities or celebrities. After a college course or two, it’s easy to lose track of concepts. So you might look at this blog as a type of refresher sometimes.

Anticipating Turning Points in Time Series

But the real problem comes with anticipating turning points in business and economic time series. Except when modeling seasonal variation, exponential smoothing usually shoots over or under a turning point in any series it is modeling.

If this were easy to correct, macroeconomic forecasts would be much better. The following chart highlights the poor performance, however, of experts contributing to the quarterly Survey of Professional Forecasters, maintained by the Philadelphia Fed.

So, the red line is the SPF consensus forecast for GDP growth on a three quarter horizon, and the blue line is the forecast or nowcast for the current quarter (there is a delay in release of current numbers). Notice the huge dips in the current quarter estimate, associated with four recessions 1981, 1992, 2001-2, and 2008-9. A mere three months prior to these catastrophic drops in growth, leading forecasters at big banks, consulting companies, and universities totally missed the boat.

This is important in a practical sense, because recessions turn the world of many businesses upside down. All bets are off. The forecasting team is reassigned or let go as an economy measure, and so forth.

Some forward-looking information would help business intelligence focus on reallocating resources to sustain revenue as much as possible, using analytics to design cuts exerting the smallest impact on future ability to maintain and increase market share.

Hedgehogs and Foxes

Nate Silver has a great table in his best-selling The
Signal and the Noise on the qualities and forecasting performance of hedgehogs and foxes. The idea comes from a Greek poet, “The fox knows many little things, but the hedgehog knows one big thing.”

Following Tetlock, Silver finds foxes are multidisplinary, adaptable, self-critical, cautious, and empirical, tolerant of complexity. By contrast, the Hedgehog is specialized, sticks to the same approaches, stubbornly adheres to his model in spite of counter-evidence, is order-seeking, confident, and ideological. The evidence suggests foxes generally outperform hedgehogs, just as ensemble methods typically outperform a single technique in forecasting.

Message – be a fox.

So maybe this can explain some of the breadth of this blog. If we have trouble predicting GDP growth, what about forecasts in other areas – such as weather, climate change, or that old chestnut, sun spots? And maybe it is useful to take a look at how to forecast all the inputs and associated series – such as exchange rates, growth by global region, the housing market, interest rates, as well as profits.

And while we are looking around, how about brain waves? Can brain waves be forecast? Oh yes, it turns out there is a fascinating and currently applied new approach called neuromarketing, which uses headbands and electrodes, and even MRI machines, to detect deep responses of consumers to new products and advertising.

New Methods

I know I have not touched on cluster analysis and classification, areas making big contributions to improvement of business process. But maybe if we consider the range of “new” techniques for predictive analytics, we can see time series forecasting and analysis of customer behavior coming under one roof.

There is, for example, this many predictor thread emerging in forecasting in the late 1990’s and especially in the last decade with factor models for macroeconomic forecasting. Reading this literature, I’ve become aware of methods for mapping N explanatory variables onto a target variable, when there are M<N observations. These are sometimes called methods of data shrinkage, and include principal components regression, ridge regression, and the lasso. There are several others, and a good reference is The Elements of Statistical Learning, Data Mining, Learning and Prediction, 2nd edition, by Trevor Hastie, Robert Tibshirani, and Jerome Friedman. This excellent text is downloadable, accessible via the Tools, Apps, Texts, Free Stuff menu option located just to the left of the search utility on the heading for this blog.

There also is bagging, which is the topic of the previous post, as well as boosting, and a range of decision tree and regression tree modeling tactics, including random forests.

I’m actively exploring a number of these approaches, ginning up little examples to see how they work and how the computation goes. So far, it’s impressive. This stuff can really improve over the old approaches, which someone pointed out, have been around since the 1950’s at least.

It’s here I think that we can sight the on-coming wave, just out there on the horizon – perhaps hundreds of feet high. It’s going to swamp the old approaches, changing market research forever and opening new vistas, I think, for forecasting, as traditionally understood.

I hope to be able to ride that wave, and now I put it that way, I get a sense of urgency in keeping practicing my web surfing.

Hope you come back and participate in the comments section, or email me at [email protected]

Business Forecasting